
P48 习题 2.2 1、2
教后感:
今天我们一起探索了数学的有关什么知识?你取得了哪些收获?
P47 练习 1,2
(二) 标准差
1.问题:
方差的单位与愿数据的单位相同吗?应该如何办?
2.引出新知----标准差概念
有些情况下,需用到方差的算术平方根,即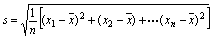 ④
④
并把它叫做这组数据的标准差.它也是一个用来衡量一组数据的波动大小的重要的量. 例如:P 47
3.教师引导学生分析方差与标准差的区别与联系:
计算标准差要比计算方差多开一次平方,但它的度量单位与原数据一致,有时用它比较方便
(一) 方差
1.描述一组数据的离散程度可采取许多方法,在统计中常先求这组数据的平均数,再求这组数据与平均数的差的平方和的平均数,用这个平均数来衡量这组数据的波动大小:
设在一组数据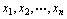 中,各数据与它们的平均数
中,各数据与它们的平均数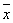 的差的平方分别是
的差的平方分别是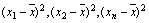 ,那么我们求它们的平均数,即用
,那么我们求它们的平均数,即用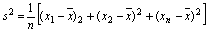
2. 请你归纳一下方差概念,并说说公式中每一个元素的意义。
3. 谈谈方差的作用?
4. 说说你的疑问:
(1)为什么要这样定义方差?
(2)为什么对各数据与其平均数的差不取其绝对值,而要将它们平方?
(3)为什么要除以数据个数n?(是为了消除数据个数的影响).
5. 初步运用
在学生理解了方差概念之后,再回到了引例中,通过计算两组数据的方差,再根据理论说明。
通过计算发现极差只能反映一组数据中两个极值之间的大小情况,而对其他数据的波动情况不敏感。让我们一起来做下列的数学活动:
1画一画
2填一填
A厂
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
|
数据 |
|
|
|
|
|
|
|
|
|
|
|
与平均值差 |
|
|
|
|
|
|
|
|
|
|
B厂
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
|
数据 |
|
|
|
|
|
|
|
|
|
|
|
与平均值差 |
|
|
|
|
|
|
|
|
|
|
3算一算
把所有差相加,把所有差取绝对值相加,把这些差的平方相加。
4想一想
你认为哪种方法更能明显反映数据的波动情况?
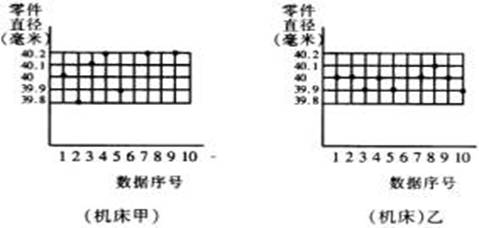
乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测。结果如下(单位:mm):
A厂:40.0,39.9,40.0,40.1,40.2,39.8,40.0,39.9,40.0,40.1;
B厂:39.8,40.2,39.8,40.2,39.9,40.1,39.8,40.2,39.8,40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
(1) 请你算一算它们的平均数和极差。
(2) 是否由此就断定两厂生产的乒乓球直径同样标准?
今天我们一起来探索这个问题。
P48 习题2.2 1、2
2、方差或标准差越大,数据的波动越大,方差或标准差越小,数据的波动越小。
1、方差与标准差的公式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com