4．小结

　　 (1)你如何判断一个三角形是不是直角三角形?

　　 (2)-一个三角形3边的大小与三角形的形状有内在联系吗?如果有，你能举例说明吗?

3．例题教学

　　 课本没有编排例题，教学中可以选用“练习”或习题2．2中的问题作为例题，以帮助学生正确应用勾股定理和直角三角形的判定条件，发展学生有条理地思考和表达的能力．

2．探索活动

　　 问题一　 请你任意挑选课本图2-5中的一组数，计算这组数中某两个数的平方和是否等于第三个数的平方?

　　 问题二　 以这组数为3边的边长画△ABC，△ABC是直角三角形吗?

　　 问题三　 你是如何说明△ABC是直角三角形的?与同学交流．

　　 实际教学中学生通常用小丽的方法来说明△ABC是直角三角形．小明的说理则是为以后(用“同一法”)证明勾股定理逆定理作铺垫．教学时可以引导学生尝试用已有的知识和经验寻求解决问题的不同方法，使学生不断获得解决问题的经验．

1．情境创设

　　 课本以古巴比伦泥板上神秘的数组揭示着什么奥秘?引入“三角形的3边a、b、c，如果满足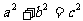，那么这个三角形是否是直角三角形”的问题，以激发学生探索研究这个问题的兴趣．

　　 教学中也可从“请你画一个3边分别是3、4、5的三角形，你有什么发现”引入“直角三角形的判定条件”的探究．

3．经历探索一个三角形是直角三角形的条件的过程，发展合情推理能力，体会“形”与“数”的内在联系．

[教学过程]

2．会应用直角三角形的判定条件判定一个三角形是直角三角形．

1．会阐述直角三角形的判定条件(勾股定理的逆定理)．　

2．2神秘的数组

[教学目标]

5．已知抛物线y＝ax²+bx+c与直线y＝x－2相交于(m，－2)，(n，3)两点，且抛物线的对称轴为直线x＝3，求函数的关系式。

4．已知抛物线y₁＝x²+x－k与直线y＝－2x+1的交点的纵坐标为3。

　　 (1)求抛物线的关系式；

　　 (2)求抛物线y＝x²+x－k与直线y＝－2x+1的另一个交点坐标．