
1.图象都是抛物线.
4.y=x2有最低点,y=-x2有最高点.
相同点:
3.在y=x2中y有最小值,即x=0时.y最小=0,在y=-x2中y有最大值.即当x=0时,y最大=0.
2.函数值随自变量增大的变化趋势不同,在y=x2图象中,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大.在y=-x2的图象中正好相反.
我们分别作出函数y=x2与y=-x2的图象,并对图象的性质作系统的研究.现在我们再来比较一下它们图象的异同点.
投影片:(§2.2 D)
不同点:
1. 开口方向不同,y=x2开口向上,y=-x2开口向下.
投影片:(§2.2 C)
二次函数y=-x2的图象是什么形状?先想一想,然后作出它的图象.它与二次函数y=x2的图象有什么关系?与同伴进行交流.
[师]请大家按照画图象的步骤作出函数y=-x2的图象.
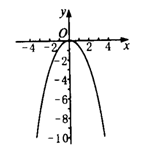 [生]y=-x2的图象
[生]y=-x2的图象
如右图:
形状还是抛物线,只
是它的开口方向向下,它
与y=x2的图象形状相同,
方向相反,这两个图形可
以看成是关于x轴对称.
[师]下面我们试着讨论y=-x2的图象的性质.
[生](1)它的开口方向向下.
(2)它的图象有最高点,最高点坐标为(0,0).
(3)它是轴对称图形,对称轴是y轴,在对称轴左侧,y随x的增大而增大,在对称轴右侧x随x的增大而减小.
(4)图象与x轴有交点,也叫抛物线的顶点,还是图象的最高点,这点的坐标为(0,0).
(5)因为图象有最高点,所以函数有最大
值,当x-0时,y最大=0.
[师]大家总结得非常棒.
投影片:(§2.2 B)
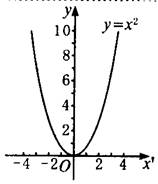
[师]从图象来看抛物线的开口方向向上.
下面请大家讨论之后系统地总结出y=x2的图象的所有性质.
[生](1)抛物线的开口方向是向上.
(2)它的图象有最低点,最低点坐标是(0,0).
(3)它是轴对称图形,对称轴是y轴.在对称轴左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大.
(4)图象与x轴有交点,这个交点也是对称轴与抛物线的交点,称为抛物线的顶点,同时也是图象的最低点,坐标为(0,0).
(5)因为图象有最低点,所以函数有最小值,当x=0时,y最小=0.
投影片:(§2.2 A)
对于二次函数y=x2的图象,
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象与x轴有交点吗?如果有,交点坐标是什么?
(3)当x<0时,随着x值的增大,y的值如何变化?当x>0时呢?
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴进行交流.
[生](1)图象的形状是一条曲线.就像抛出的物体所行进的路线的倒影.
(2)图象与x轴有交点,交于原点,交点坐标是(0,0).
(3)当x<0时,图象在y轴的左侧,随着x值的增大,y的值逐渐减小;当x>0时,图象在y轴的右侧,随着x值的增大,y的值逐渐增大。
(4)观察图象可知,当x=0时,y的值最小,最小值是0.
(5)由图可知,图象是轴对称图形,它的对称轴是y轴,从刚才的列表中可找到对应点(-1,1)和(1,1);(-2,4)和(2,4);(-3,9)和(3,9).
[师]大家的分析判断能力很棒,下面我们系统地总结一下.
[师]一次函数的图象是一条直线,二次函数的图象是什么形状呢?让我们先看最简单的二次函数y=x2.
大家还记得画函数图象的一般步骤吗?
[生]记得,是列表,描点,连线.
[师]非常正确,下面就请大家按上面的步骤作出y=x2的图象.
[生](1)列表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
(2)在直角坐标系中描点.
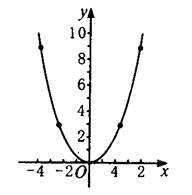
(3)用光滑的,曲线连接各点,便得到函数y=x2的图象.
[师]画的非常漂亮.
5. 函数y=x2与y=-x2的图象的比较
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com