2．议一议(投影片§2．2 A)

3．比较y＝x²与y=-x²的图象的异同点及联系．

　　 Ⅴ．课后作业

　　 习题2．2

　　 Ⅵ．活动与探究

　　 已知函数y=m·x^m2+m．

　　 m取何值时，它的图象开口向上．

　　 当x取何值时，y随x的增大而增大．

　　 当x取何值时，y随x的增大而减小．

　　 x取何值时，函数有最小值．

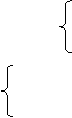　　　　　　　 M≠0

解：由题意得：

　　　　　　　 m²+m=2

　　　 m≠0

解得　　

m=1或m=-2

　　 当m=-2时，y=-2x²开口向下

　　 ∴m=1

　　 即当m=1时，它的图象是开口向上的抛物线．

　　 函数关系式为y=x²．

　　 当x>0时，y随x的增大而增大．

　　 当x<0时，y随x的增大而减小．

　　 当x=0时，函数有最小值．

板书设计

§2．2　 结识抛物线

2．画函数y＝-x²的图象，并研究其性质．

1．画函数y=x²的图象，并对图象的性质作了总结．

3．解：抛物线y＝4x2的开口向上，对称轴是y轴，顶点是原点，坐标为(0，0)．

　　 抛物线y＝-x²的开口向下，对称轴是y轴，顶点坐标为(0，0)．

　　 Ⅳ．课时小结

　　 本节课我们学习了如下内容：

3．分别说出抛物线y=4x²与y＝- 　x²的开口方向，对称轴与顶点坐标．

　　 答案：1．略　 2．A

2．下列函数中是二次函数的是　 (　　 )

　　 A. y=2+5x²

　　 B．y=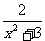

　　 C．y＝3x(x+5)²

　　 D. y=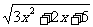

1．在同一直角坐标系中画出函数y=x²与y=-x²的图象．

3．图象都关于y轴对称．

联系：

它们的图象关于x轴对称．

　　 Ⅲ．课堂练习

2．图象都与x轴交于点(0，0)．