
2.ab减去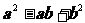 等于 ( )。
等于 ( )。
A.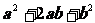 ; B.
; B.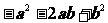 ;C.
;C.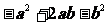 ;D.
;D.
1.下列说法中正确的是( )。
A.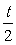 不是整式; B.
不是整式; B. 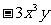 的次数是
的次数是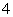 ;C.
;C.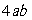 与
与 是同类项; D.
是同类项; D.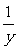 是单项式
是单项式
2.3 整式的加减教学设计
|
教 材 分 析 |
本节课的教学内容去括号是中学数学代数部分的一个基础知识点,是以后化简代数式、分解因式、配方法等知识点中的重要环节。对于七年级学生来说接受该知识点存在一个思维上的转换过程。所以又是一个难点,由此不难看出,该知识点在初中数学教材中有其特殊地位和重要作用。 |
||
|
学法 引导 |
1、教学方法:发现尝试法。充分体现学生的主体作用。 2、学生学法:练习 去括号法则 练习巩固 3、引导学生由数及式,由特殊到一般,由一般到特殊学习。并由此突破难点。 |
||
|
教 学 目 标 |
知识目标 |
1、掌握去括号法则。 2、应用去括号法则,能按要求去括号。 |
|
|
能力目标 |
1、通过去括号法则的应用,培养学生全方位考虑问题的能力,不要只考虑括号内的部分项,而要考虑括号内的每一项。 2、通过去括号法则的推导,培养学生观察能力和归纳知识的能力。 |
||
|
素养目标 |
1、渗透从特殊到一般和从一般到特殊的数学思想,培养初步的辩证唯物主义观点。 2、去括号使代数式中符号简化,也便于合并同类项,体现了数学的简洁美。 |
||
|
教学重点 |
去括号法则及其应用 |
||
|
教学难点 |
括号前面是“-”号的去括号法则 |
||
|
教学过程设计 |
|||
|
教学流程 |
教师活动 |
学生活动 |
|
|
一、复习引入 创设情境 |
1、提出问题:什么是同类项?同类项有哪两个特征? 2、用小黑板出示: 下列各题中的两项是不是同类项? 1)x与y 2)a2b与ab2 3)-3pq与3pq 4)abc与ac 5)a与a 6)53与-24 3、合并下列各式中的同类项: 1)4a2+3b2+2ab-4a2-3b2 2) 4x2+2x-1-3x2+3x+2 4、提出问题:多项式(2ab-πr2)-(ab-πr2)中有同类项吗?如何合并? 5、共同归纳:要去掉括号,板书课题。 |
思考 回答 练习 板演 讨论 思考 回答 |
|
|
二、 探索 新知 讲授 新课 |
1、提出问题:如何去括号呢? 2、小黑板出示:请大家计算下列各题,并观察所得结果。 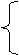 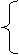 13+(7-5)
13-(7-5) 13+(7-5)
13-(7-5)13+7-5 13-7+5 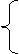 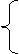 9a+(6a-a) 9a-(6a-a) 9a+(6a-a) 9a-(6a-a)9a+6a-a 9a-6a+a 3、提出问题:通过上面的计算,你发现了什么?两种运算有何区别? 4、总结:从以上计算可以看出,按照两种不同的运算顺序,所得结果相同,即去括号时不能改变原式的值。 5、提出问题:上面四组式子,每组式子左边都有括号,并且括号前面有“+”号、“-”号,而右边没有括号,比较右边相应项的符号的变化,你能归纳出去括号的法则吗? 6、归纳并板书。 1)括号前面是“+”号,把括号连同它前面的“+”号去掉,括号里各项不变符号。 2)括号前面是“-”号,把括号连同它前面的“-”号去掉,括号里各项都变号。 7、强调: 1)各项不变符号、改变符号的含义。 2)括号连同前面的符号一起去掉。 8、算理说明: (2ab-πr2)=(+1)×(2ab-πr2) =(+1)×2ab-(+1)×πr2 =2ab-πr2 -(ab-πr2)=(-1)×(ab-πr2) =(-1)×ab-(-1)×πr2 =- ab+πr2 去括号运算的依据是分配律。 |
计算 回答 同桌讨论 指名回答 同桌讨论 找语言表达能力强的学生叙述 |
|
|
|
9、巩固法则: 例1:去括号 1)a+(-b+c-d) 2)a-(-b+c-d) 3)-(p+q)+(m-n) 4)(r+s)-(p-q) 5)a-2(b+c) 6)a+3(2b+c) 例2:先去括号,再合并同类项: 1)8a+2b+(5a-b) 2) a+(5a-2b)-2(a-2b) 3) 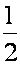 (a+4b)- (a+4b)- 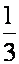 (3a-6b) (3a-6b)4)x+[x+(-2x-4y)] 归纳:①易错的地方,错误的原因。 ②怎样防止错误。 |
练习本上 完成板演 相互评分订正 板演 练习 评分 订正 |
|
三、巩固练习 尝试反馈 |
布置P73-74练习 巡视,个别指导 |
练习 |
|
四、归纳 总结 |
本节课我们学习了去括号法则,下面我们一起回顾这一法则: 1、括号前面是“+”号,把括号连同它前面的“+”号去掉,括号里各项不变符号。 2、括号前面是“-”号,把括号连同它前面的“-”号去掉,括号里各项都变号。 |
|
|
五、布置作业 |
P76 习题2.3 第4、7题 |
|
 =0,x
=0,x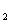 =一6.
=一6.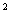 =n(n
=n(n 0).
0).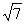 x2=5-
x2=5-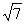
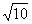 x2=-3-
x2=-3-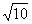
P56,习题2.5,1、2
3、一元二次方程的解一般有两个,要根据实际情况舍去不合题意的解。
2、设计方案时,关键是列一元二次方程。
1、本节内容的设计方案不只一种,只要合符条件即可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com