2.补充练习：把下列各式分解因式：

(1)(x+y)²+6(x+y)+9;

(2)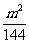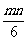－+n²;

(3)4(2a+b)²－12(2a+b)+9;

(4)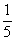x²y－x⁴－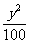

1.随堂练习见书本

=－［x²－2·x·2y+(2y)²］

2.例题讲解

［例1］把下列完全平方式分解因式：

(1)x²+14x+49;

(2)(m+n)²－6(m +n)+9.

分析：大家先把多项式化成符合完全平方公式特点的形式，然后再根据公式分解因式.公式中的a,b可以是单项式，也可以是多项式.

解：(1)x²+14x+49=x²+2×7x+7²=(x+7)²

(2)(m +n)²－6(m +n)+9=(m +n)²－2·(m +n)×3+3²=［(m +n)－3］²=(m +n－3)².

［例2］把下列各式分解因式：

(1)3ax²+6axy+3ay²;(2)－x²－4y²+4xy.

分析：对一个三项式，如果发现它不能直接用完全平方公式分解时，要仔细观察它是否有公因式，若有公因式应先提取公因式，再考虑用完全平方公式分解因式.

如果三项中有两项能写成两数或式的平方，但符号不是“+”号时，可以先提取“－”号，然后再用完全平方公式分解因式.

解：(1)3ax²+6axy+3ay²

=3a(x²+2xy+y²)

=3a(x+y)²

(2)－x²－4y²+4xy

1.推导用完全平方公式分解因式的公式以及公式的特点.

由因式分解和整式乘法的关系，大家能否猜想出用完全平方公式分解因式的公式呢？

将完全平方公式倒写：

a²+2ab+b²=(a+b)²;

a²－2ab+b²=(a－b)².

便得到用完全平方公式分解因式的公式.

请大家互相交流，找出这个多项式的特点.

从上面的式子来看，两个等式的左边都是三项，其中两项符号为“+”，是一个整式的平方，还有一项符号可“+”可“－”，它是那两项乘积的两倍.凡具备这些特点的三项式，就是一个二项式的完全平方，将它写成平方形式，便实现了因式分解.

左边的特点有(1)多项式是三项式；

(2)其中有两项同号，且此两项能写成两数或两式的平方和的形式；

(3)另一项是这两数或两式乘积的2倍.

右边特点：这两数或两式和(差)的平方.

用语言叙述为：两个数的平方和，加上(或减去)这两数的乘积的2倍，等于这两个数的和(或差)的平方.

形如a²+2ab+b²或a²－2ab+b²的式子称为完全平方式.

由分解因式与整式乘法的关系可以看出，如果把乘法公式反过来，那么就可以用来把某些多项式分解因式，这种分解因式的方法叫做运用公式法.

练一练.下列各式是不是完全平方式？

(1)a²－4a+4;

(2)x²+4x+4y²;

(3)4a²+2ab+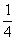b²;

(4)a²－ab+b²;

2．随着改革开放，市场经济不向发展，许多农民走上了致富的门道路。《新华日报》1994年3月18B报道了江苏省金湖县塔泉乡对坝村王兴国利用一幢旧平房改建成免舍成为十万元户的消息．王兴国的旧平房墙长16米，若欲再利用一面墙扩建一面积为150平方米的长方形免舍，现有的材料可供这另三面墙共35米长，问免舍的长与宽各为多少米？

随堂练习：

随堂练习1、2

课堂小结：

公式法实际上是配方法的一般化和程式化，利用公式法可以较为简便地解一元二次方程。

作业：

课本习题2．6　 1、2

1．用篱笆国成一个长方形菜地，其中一面靠墙，且在与墙平行的一边开一扇2米宽的门，如果墙长50米，现有能围成91米长的篱笆，菜地的面积需要1080平方米，求菜地的长和宽．

3．关键：运用配方法推导出一元二次方程的求根公式。

教学过程：

问题：你能用配方法解方程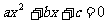吗？

通过推导得出答案：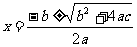

例题：

2．难点；对公式法中求根公式的推导过程的理解．