
备课资料
参考练习
1.在同一直角坐标系内画出下列函数的图象:
(1)y=3x2 (2)y=-3x2 (3)y= x2
x2
答案:略
4.议一议(投影片§2.3 C)
3.做一做(投影片§2.3 B)
2.比较s= v2与s=
v2与s=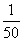 v2的图象
v2的图象
投影片:(§2.3 C)
(1)在同一直角坐标系内作出函数y=2x2与y=2x2+1的图象.并比较它们的性质.
(2)在同一直角坐标系内作出函数y=3x2与y=3x2-1的图象,并比较它们的性质.
(3)由上可得出什么?
[生](1)图象如下:

比较性质如下:
相同点:
a.它们的图象都是抛物线,且形状相同,开口方向相同.
b.它们都是轴对称图形,且对称轴都是y轴.
c.在y轴左侧,y随x的增大而减小;在y轴右侧,y随x的增大而增大.
d.都有最低点,y都有最小值.
不同点:
a.它们的顶点不同,y=2x2的顶点在原点,坐标为(0,0);y=2x2+1的顶点在y轴上,坐标为(0,1).
b.虽然函数y都有最小值,但y=2x2的最小值为0,y=2x2+1的最小值为1.
联系;
y=2x2+1的图象可以看成函数y=2x2的图象整体向上平移一个单位.
(2)[生]y=3x2与y=3x2-1的图象如下
:
性质比较如下:
相同点:
a.它们的图象都是抛物线,且形状相同,开口方向相同.
b.它们都是轴对称图形,且对称轴都是y轴.
c.都有最低点,函数值都有最小值.
d.在y轴左侧,y都是随x的增大而减小,在y轴右侧,y都随x的增大而增大.
c.它们的增长速度相同.
不同点:
a.它们的顶点不同y=3x2的顶点在原点,坐标为(0,0),y=3x2-1的顶点在y轴上,坐标为(0,-1).
b.y=3x2的最小值为0,y=3x2-1的最小值为-1.
联系:y=3x2-1的图象可以看成是y=3x2的图象整体向下平移一个单位.
[生](3)可以知道y=2x2+1的图象是y=2x2的图象整体向上移动一个单位得到的.
[师]是的.由上可知,y=ax2与y=ax2+c的图象形状相同,开口方向相同,对称轴也相同,只是顶点不同,函数的最大值或最小值不同.y=ax2+c的图象可以看成y=ax2的图象整体上下移动得到的,当c>O时,向上移动│c│个单位,当c<0时,向下移动│c│个单位.
Ⅲ.课堂练习
画出函数y= x2与y=2x2的图象.(在同一直角坐标系内)并比较它们的性质.
x2与y=2x2的图象.(在同一直角坐标系内)并比较它们的性质.
分析:画函数图象的步骤有列表、描点、连线.
解:
|
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
y= x2 x2 |
8 |
4.5 |
2 |
0.5 |
0 |
0.5 |
2 |
4.5 |
8 |
|
x |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
|
y=2x2 |
8 |
4.5 |
2 |
0.5 |
0 |
0.5 |
2 |
4.5 |
8 |
分别描点画图.
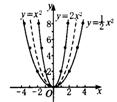
相同点:图象都是抛物线,开口方向相同、顶点相同,都有最低点,函数有最小值.y
的值随x的增大而变化情况相同.
不同点:抛物线的开口大小不同,函数值的增长速度不同.
Ⅳ.课时小结
本节课巩固了画函数图象的步骤:列表、描点、连线;学习了刹车距离与二次函数的关
系;并比较了函数y=2x2与y=x2,y=2x2+1与y=2x2,y=3x2-1与y=3x2的图象的性质.
Ⅴ.课后作业
习题2.3
Ⅵ,活动与探究
略
板书设计
§2.3 刹车距离与二次函数
投影片:(§2.3 B)
作二次函数y=2x2的图象.
(1)完成下表:
|
x |
|
|
|
|
|
|
|
|
2x2 |
|
|
|
|
|
|
|
(2)在下图中作 出y=2x2的图象.
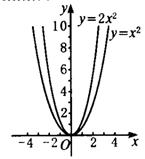
(3)二次函数y=2x2的图象是什么形状?它与二次函数y=x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
[生](1)略 (2)如图
(3)二次函数y=2x2的图象是抛物线.
它与二次函数y=x2的图象的相同点:
开口方向相同,都向上.
对称轴都是y轴.
顶点都是原点,坐标为(0,0).
在y轴左侧,都是y值随x值的增大而减小;在y轴右侧,都是y值随x值的增大而增大.
都有最低点,即原点.
函数都有最小值.
不同点:y=2x2的图象在y=x2的图象的内侧.
y=2x2中函数值的增长速度较快.
[师]从上图中,大家可以互相讨论图象有什么相同与不同?
[生]相同点:
(1)它们都是抛物线的一部分
(2)二者都位于s轴的左侧.
(3)函数值都随v值的增大而增大.
不同点:
(1)s=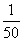 v2的图象在s=
v2的图象在s=  v2的图象的内侧.
v2的图象的内侧.
(2)s= 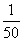 v2的s比s=
v2的s比s=  v2中的S增长速度快.
v2中的S增长速度快.
[师]如果行车速度是60 km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?
[生]已知v=60 km/h.分别代入s=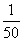 v2与s=
v2与s= v2中.相应地求出各自的刹车
v2中.相应地求出各自的刹车
距离,再求它们的差,即s1= 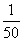 × 602=72,
× 602=72,
s2  ×602=36.则
×602=36.则
s1-s2=72-36=36(m).
所以在雨天行驶和在晴天行驶相比,雨天的刹车距离较长,相差36 m.
[师]大家知道两辆车在行驶时为什么要保持一定距离吗?
[生]怕发生“迫尾”事故.
[师]汽车刹车时向前滑行的离与什么因素有关呢?
[生]与汽车行驶的速度有关系.
[师]究竟与什么有关,关系有多大呢?
投影片:(§2.3 A)
影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数.有研究表明,晴
天在某段公路上行驶时,速度为v(km/h)的汽车的刹车距离s(m)可以由公式s= v2
v2
确定,雨天行驶时,这一公式为s=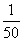 v2.
v2.
[师]引刹车距离s与速度v之间的关系是二次函数吗?
[生]根据二次函数的定义可知,它们都是二次函数.
[师]与一上节课中学习的二次函数y=x2和y=-x2有什么不同吗?
[生]y=x2中的a为1.
s=  v2中的a为
v2中的a为 .
.
所以它们的不同之处在于a的取值不同.
[师]很好.
既然s= v2和s=
v2和s=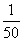 v2与y=x2,y=-x2它都是二次函数,且都是只含二次项的二次函数,所以它们有相同之处;又因为它们中的a值的不同.所以它们肯定还有不同之处.比如在y=x2中自变量x可以取正数或负数,在s=
v2与y=x2,y=-x2它都是二次函数,且都是只含二次项的二次函数,所以它们有相同之处;又因为它们中的a值的不同.所以它们肯定还有不同之处.比如在y=x2中自变量x可以取正数或负数,在s= v2中,因为v是速度,能否取负值呢?由实际情况可知”不可以取负值.
v2中,因为v是速度,能否取负值呢?由实际情况可知”不可以取负值.
下图是s= v2的图象,根据画图象的三个步骤即列表、描点、连线,在同一直角坐
v2的图象,根据画图象的三个步骤即列表、描点、连线,在同一直角坐
标系内作出函数s=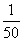 v2的图象.
v2的图象.

13.如图,AB是高为1.46米的窗户(窗户朝南),该窗户的遮阳篷呈抛物线形, 在图中坐标系内的表达式为y=-x2+0.25. 已知该地一年中冬至日正午时刻太阳光线与地面的夹角最小为α,夏至日正午时刻太阳光线与地面的夹角最大为β,且β=73°30′. 若该遮阳篷使冬至日正午时刻太阳光线刚好全部射入室内, 夏至日正午时刻太阳光刚好全部不射入室内.求α的度数及遮阳篷顶部到窗户上沿的距离.

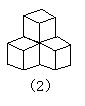
12.图(1)是棱长为a的小正方体,图(2)、图(3)这样的小正方体摆放而成,按照这样的方法继续摆放,自上而下分别叫第一层、第二层……第n层,第n层的小正方体的个数记为s,解答下列问题:
(1)按要求填表:
|
n |
1 |
2 |
3 |
4 |
… |
|
s |
1 |
3 |
|
|
… |
(2)写出n=10时,s=________.
(3)根据上表中的数据,把s作为点的纵坐标,n作为点的横坐标,在平面直角坐标系中描出相应的点.
(4)请你猜一猜上述各点会在某一函数图像上吗?如果在某一函数的图像上, 求s与n间的关系.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com