
1.抛物线y=-4x2-4的开口向 ,当x= 时,y有最 值,y= .
[例1] 已知抛物线y=(m+1)x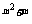 开口向下,求m的值.
开口向下,求m的值.
[例2]k为何值时,y=(k+2)x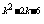 是关于x的二次函数?
是关于x的二次函数?
[例3]在同一坐标系中,作出函数①y=-3x2,②y=3x2,③y= x2,④y=-
x2,④y=- x2的图象,并根据图象回答问题:(1)当x=2时,y=
x2的图象,并根据图象回答问题:(1)当x=2时,y= x2比y=3x2大(或小)多少?(2)当x=-2时,y=-
x2比y=3x2大(或小)多少?(2)当x=-2时,y=- x2比y=-3x2大(或小)多少?
x2比y=-3x2大(或小)多少?
[例4]已知直线y=-2x+3与抛物线y=ax2相交于A、B两点,且A点坐标为(-3,m).
(1)求a、m的值;
(2)求抛物线的表达式及其对称轴和顶点坐标;
(3)x取何值时,二次函数y=ax2中的y随x的增大而减小;
(4)求A、B两点及二次函数y=ax2的顶点构成的三角形的面积.
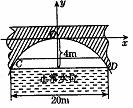 [例5]有一座抛物线形拱桥,正常水位时,桥下水面宽度为20m,拱顶距离水面4m.(1)在如图所示的直角坐标系中,求出该抛物线的表达式;(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出将d表示为k的函数表达式;(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
[例5]有一座抛物线形拱桥,正常水位时,桥下水面宽度为20m,拱顶距离水面4m.(1)在如图所示的直角坐标系中,求出该抛物线的表达式;(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出将d表示为k的函数表达式;(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
2.在同一平面内画出函数y=3x2与y=3x2-1的图象。
比较它们的性质,你可以得到什么结论?
1.在同一平面内画出函数y=2x2与y=2x2+1的图象。
你知道两辆汽车在行驶时为什么要保持一定距离吗?
刹车距离与什么因素有关?
有研究表明:汽车在某段公路上行驶时,速度为v(km/h)汽车的刹车距离s(m)可以由公式:
晴天时: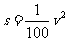 ;雨天时:
;雨天时: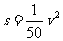 ,请分别画出这两个函数的图像:
,请分别画出这两个函数的图像:
二次函数y=x2 与y=-x2的性质:
|
抛物线 |
y=x2 |
y=-x2 |
|
对称轴 |
|
|
|
顶点坐标 |
|
|
|
开口方向 |
|
|
|
位置 |
|
|
|
增减性 |
|
|
|
最值 |
|
|
4.函数y=-5x2有最大值或最小值吗?如果有,是最大值还是最小值?这个值是多少:
答案:函数y=-5x2有最大值,这个值是0.
3.函数y=5x2的图象在对称轴哪侧?y随着x的增大怎样变化?
答案:函数y=5x2的图象在对称轴右侧部分.y随着x的增大而增大.
2.分别说出抛物线y=4x2与y=-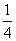 x2的开口方向、对称轴与顶点坐标.
x2的开口方向、对称轴与顶点坐标.
答案:y=4x2的开口方向向上,对称轴为y轴.顶点坐标为(0,0).
备课资料
参考练习
1.在同一直角坐标系内画出下列函数的图象:
(1)y=3x2 (2)y=-3x2 (3)y=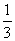 x2
x2
答案:略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com