9.9　 10.3　 9.8　 10.1　 10.4　 10　 9.8　 9.7

　　 (2)甲、乙两人在相同条件下各掷铁饼5次，距离如下；(单位：米)

　　 甲：46.0　 48.5　 41.6　 46.4　 45.5

　　 乙：47.1　 40.8　 48.9　 48.6　 41.6

　 　(1)试判定谁投的远一些?

　 　(2)说明谁的技术较稳定?

2．补充：(1)用计算器求下面一组数据的标准差：

1．P50练习

教师巡视指导。

下面以计算P.49的问题为例。

为了从小明和小丽两人中选拔一个参加学校军训射击比赛，现对他们的射击成绩进行了测试，10次打靶命中的环数如下：

小明：10，7，8，8，8，8，8，8，9，6；

小丽： 8，8，8，8，5，8，8，9，9，9

计算小明和小丽命中环数的方差和标准差，哪一个人的射击成绩比较稳定？

方法一：

(1)打开计算器；

(2) 2ndF　 MODE　1进入统计状态；

(3) 10　DATA　7　DATA　8　DATA　…6　DATA输入所有数据；；

(4) SHIFT　X-M　＝计算这组数据的方差。

(5)SHIFT　RM　＝计算这组数据的标准差。

说明：

(1)按DATA　DATA键可输入两次同样的数据。

(2)输入10次110时，可按110　SHIFT　 : 　10 　DATA键。

(3)需要删除刚输入的数据时，可按SHIFT　CL键。

方法二：见P50中“方法二”

2．极差、方差与标准反映了一组数据的什么?

引入：用笔算的方法计算标准差比较繁琐，如果能够利用计算器，就会大大提高效率。那么本节就来学习用计算器求标准差。

1．什么是极差?什么是方差与标准差?

4．小结

　　 (1)你能说出一些数的平方根与算术平方根吗?

　　 (2)算术平方根与平方根有什么区别与联系?

3．思维拓展

　　 “讨论”和练习第3题都可以作为思维拓展的材料．教学中应较多地关注学生解决这类问题的不同思维策略．学生在解决问题过程中可能表现出以下的不同水平：

　　 (1)依据算术平方根的定义求解；

　　 (2)从开平方与平方互为逆运算的角度求解；

(3)从这一类具体例子的求解中归纳概括出一般形式：

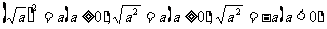
　 教师要尊重学生在解决问题中表现出的不同水平，让学生交流各自解决问题的策略，不断获得解决问题的经验，提高思维水平．不要把归纳概括出一般形式作为本节课思维拓展的主要目标．

2．例题教学

　　 (1)例2仍采用符号结合文字语言叙述的写法，以利于学生加深对开平方与平方互为逆运算关系的理解，并便于仿照例1的书写进行练习和习题．

(2)例3是算术平方根的实际应用．教学中要鼓励学生用不同的计算方法求解，学生可能会有以下的解法：

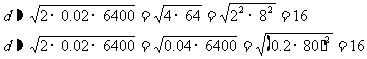
教学中应引导学生各自说明算理并交流，以加深学生对所学知识的理解．

1．情境创设

　　 本课时采用如下的问题情境：

　　 (1)现在你能计算小方格纸中边长为1的正方形对角线的长吗?面积为15m²的正方形房间的边长，4个直角边长为10cm的等腰直角三角形纸片拼合成的正方形的边长呢?

　　 (2)对这类问题的求解，你有合理化的建议吗?

创设上述情境，便于学生主动发现正的平方根为解决问题提供方便．此后再介绍算术平方根及其符号表示．