6．抛物线y=-2x²-4x+1的顶点关于x轴对称的点的坐标是__________．

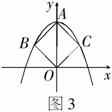
5．如图3，在平面直角坐标系中，二次函数y=ax²+c(a≠0)的图象过正方形ABOC的三顶点ABC，则ac的值是_______．

3．已知二次函数y=-x²+2x+c²的对称轴和x轴相交于点(m，0)，则m的值为__________．

　4．已知二次函数的图象开口向上，且顶点在y轴的负半轴，请你写出一个满足条件的二次函数关系式__________．

2．抛物线y=(x-1)²+3的顶点坐标为_________．

1．将抛物线y=x²向左平移4个单位后，再向下平移2个单位，则此时抛物线的函数关系式是________．

　例9　有3个二次函数，甲：y=x²-1；乙：y=-x²+1；丙：y=x²+2x-1，则下列叙述中正确的是(　)

　A ．甲的图象经过适当的平行移动后，可以与乙的图象重合

　B．甲的图象经过适当的平行移动后，可以与丙的图象重合

　C．乙的图象经过适当的平行移动后，可以与丙的图象重合

　D．甲、乙、丙3个图象经过适当的平行移动后，都可以重合

　析解：在平移的过程中，抛物线的形状始终保持不变，而抛物线的形状只与二次项系数有关，所以甲的图形经过适当的平行移动后，可以与丙的图形重合，故选B．

　专题训练(一)

　例7　在同一直角坐标系中，一次函数y=ax+b和二次函数y=ax²+bx的图象可能为(　)

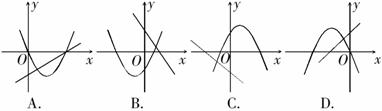
　析解：此类问题通常从比较简单的图象(直线或双曲线)出发，获得与抛物线有关的字母的取值情况，然后由字母的取值情况来判断抛物线的大致位置，如果一致则有可能共存于同一个坐标系中，如果不一致则说明是不可能共存于同一坐标系中．本题中我们先看选项A ，由于直线y=ax+b经过一、三象限，所以a＞0，又因为直线与y轴的负半轴有交点，所以b＜0；当a＞0，b＜0时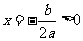，，所以抛物线y=ax²+bx的开口方向向上，对称轴在y轴的右侧，显然选项A 可能，选项B不可能．再看选项C，由于直线y=ax+b经过二、四象限，所以a＜0，又因为直线与y轴的负半轴有交点，所以b＜0；当a＜0，b＜0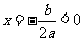，，所以抛物线y=ax²+bx的开口方向向下，对称轴在y轴的左侧，显然选项C不可能．

　再看选项D，由于直线y=ax+b经过一、三象限，所以a＞0，又因为直线与y轴的正半轴有交点，所以b＞0；当a＞0，b＞0时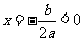，，所以抛物线y=ax²+bx应该开口方向向上，对称轴在y轴的左侧，显然选项D也是不可能的．故选A ．

　注：我们为了帮助大家掌握此类问题的解法，对每一个选项进行了一一分析．当然，在考试中我们为了节约时间，如果能够分析出选项A 是可以共存于同一个坐标系中，且四个选项中只有一个正确，那么后面的选项就不用再一一分析了．

　五、求函数关系式中参数的值

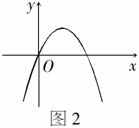
　例8　若二次函数y=ax²+2x+a²-1(a≠0)的图象如图2所示，则a的值是________．

　析解：本题是利用图象求二次函数关系式中的未知数a．由图象可知(0，0)点满足关系式y=ax²+2x+a²-1(a≠0)，代入求得a=±1．又因图象开口向下，故a=-1．

　例5　若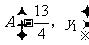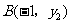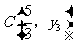，，为二次函数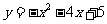的图象上的三点，则y₁、y₂、y₃的大小关系是(　)

　A ．y₁＜y₂＜y₃　　　　　　 B．y₃＜y₂＜y₁　　　　　　　　　　 C．y₃＜y₁＜y₂　　　　　　　　　　 D．y₂＜y₁＜y₃

　析解：解决此类问题的关键是求出抛物线的对称轴，由a的正负性就可以知道抛物线的增减性，如果所给的点没有在对称轴的同一侧，可以利用抛物线的对称性，找到这个点的对称点，然后根据增减性再做判断．y=-x²-4x+5配方，得y=-(x+2)²+9，因为a=-1＜0，所以当x＞-2时，y随x的增大而减小，又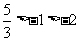，所以y₃＜y₂，又由抛物线的对称性知，y₁的值等于函数在处的函数值．因为当x＞-2时，y随x的增大而减小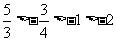，，所以y₃＜y₁＜y₂．故选C．

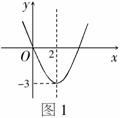
　例6　小明从图1的二次函数y=ax²+bx+c图象中，观察得出了下面的五条信息：

　①a＜0，②c=0，③函数的最小值为-3，④当x＜0时，y＞0，⑤当0＜x₁＜x₂＜2时，y₁＞y₂．你认为其中正确的个数为(　)

　A ．2　B．3　C．4　D．5

　析解：本题考查了二次函数的相关知识，观察图象可知a＞0，故①错误；因为函数图象经过原点，故c=0，②正确；③正确；④正确；⑤二次函数开口向上时，对称轴的左边，y随x的增大而减小，故⑤正确，选C．

　例4　请选择一组你喜欢的a、b、c的值，使二次函数y=ax²+bx+c(a≠0)的图象同时满足下列条件：①开口向下；②当x＜2时，y随x的增大而增大；当x＞2时，y随x的增大而减小．这样的二次函数的关系式可以是_____________．

　析解：本题考查了根据条件确定二次函数关系式的能力．根据所给条件可知这个抛物线所对应的函数关系式中的a＜0，其对称轴为x=2，则符合这两个条件的二次函数的关系式可以是y=-(x-2)²+2等．

　例1　抛物线y=3(x-1)²+1的顶点坐标是(　)

　A ．(1，1)　 B．(－1，1)　 C．(－1，－1)　 D．(1，－1)

　析解：因为二次函数y=a(x-h)²+k的顶点坐标为(h，k)，在本题中h=1，k=1，因此y=3(x-1)2+1的顶点坐标为(1，1)．故选A ．

　例2　抛物线y=2x²+4x+5的对称轴是x=__________．

　析解：由抛物线的对称轴公式，

　得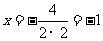，即．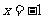

　例3　二次函数y=x²+x-6的图象与x轴交点的横坐标是(　)

　A ．2和－3　　　　　 B．－2和3　　　　　 C．2和3　　　　　　　 D．－2和－3

　析解：令y=0，则x²+x-6=0，解得x₁=2，x₂=-3．所以二次函数y=x²+x-6的图象与x轴交点的横坐标是2和－3，故选A ．