16．已知两个关于x的二次函数y₁与y₂，y₁=a(x-k)²+2(k＞0)，y₁+y₂=x²+6x+12；当x=k时，y₂=17；且二次函数y₂的图象的对称轴是直线x=-1．

　(1)求k的值．

　(2)求函数y₁、y₂的关系式．

　(3)在同一直角坐标系内，问函数y₁的图象与y₂的图象是否有交点？请说明理由．

15．抛物线y=-x²+(m-1)x+m与y轴交于(0，3)点．

　(1)求出m的值并在图6中画出这条抛物线．

　(2)求它与x轴的交点和抛物线顶点的坐标．

　(3)x取值什么值时，抛物线在x轴上方？

　(4)x取什么值时，y的值随x的增大而减小？

14．已知二次函数y=x²+4x，

　(1)利用配方法把该函数化为y=a(x-h)²+k(其中a、h、k都是常数，且a≠0)的形式，并指出函数图象的对称轴和顶点坐标．

　(2)函数图象与x轴的交点坐标．

13．求二次函数y=x²-2x-1的顶点坐标及它与x轴的交点坐标．

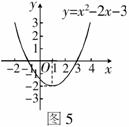
12．已知函数y=x²－2x-3的图象如图5所示，根据其中提供的信息，可求得使y≥0成立的x的取值范围是(　)

　A．-1≤x≤3　　　　　　　　　 B．-3≤x≤1

　C．x≥-3　　　　　　　　　　　 D．x≤－1或x≥3

11．二次函数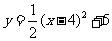的图象的开口方向、对称轴、顶点坐标分别是(　)

　A．向上、直线x＝4、(4，5)

　B．向上、直线x＝－4、(－4，5)

　C．向上、直线x＝4、(4，－5)

　D．向下、直线x＝－4、(－4，5)

10．已知y=2x²的图象是抛物线，若抛物线不动，把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线所对应的函数关系式是(　)

　A ．y=2(x-2)²+2　　　　　　 B．y=2(x+2)²-2

　C．y=2(x-2)²-2　　　　　　　 D．y=2(x+2)²+2

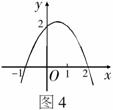
9．如图4，抛物线的函数关系式是(　)

　A ．y=x²-x+2

　B．y=-x²-x+2

　C．y=x²+x+2

　D．y=-x²+x+2

8．函数y=x²+bx-c的图象经过点(1，2)，则b-c的值为___________．

　二、选择题

7．开口向下的抛物线y=(m²-2)x²+2mx+1的对称轴经过点(－1，3)，则m=___________．