
投影片:(§2.4.2 C)
如右图,一边靠校园院墙,另外三
边用50 m长的篱笆,围起一个长
方形场地,设垂直院墙的边长为xm.
(1)写出长方形场地面积y(m2)与x的函数关系式;
(2)画出函数的图象;
(3)求边长为多少时,长方形面积最大,最大是多少?
解:(1)垂直院墙的边长为x m,另一边长为(50-2x)m.则
y=x(50-2x)=-2x2+50x=-2(x-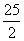 )2+
)2+ .
.
(2)图象略.
(3)由(1)得,当x=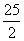 时,y最大=
时,y最大= .
.
所以当边长为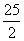 m时,长方形面积最大,最大面积为
m时,长方形面积最大,最大面积为 m2.
m2.
Ⅲ.课堂练习
1.随堂练习
投影片:(§2.4.2 B)
下图所示桥梁的两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
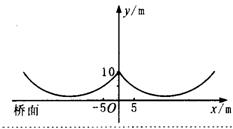
(1)钢缆的最低点到桥面的距离是多少?
(2)两条钢缆最低点之间的距离是多少?
(3)你是怎样计算的?与同伴进行交流.
分析:因为两条钢缆都是抛物线形状,且开口向上.要求钢缆的最低点到桥面的距离就是要求抛物线的最小值.又因为左右两条抛物线关于y轴对称,所以它们的顶点也关于y轴对称,两条钢缆最低点之间的距离就是两条抛物线顶点的横坐标绝对值之和或其中一条抛物线顶点横坐标绝对值的2倍.已知二次函数的形式是一般形式,所以应先进行配方化为y=a(x-h)2+k的形式,即顶点式.
解:y=0.0225x2+0.9x+10
=0.0225(x2+40x+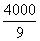 )
)
二0.0225(x2+40x+400-400+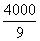 )
)
=0.0225(x+20)2+1.
∴对称轴为x=-20.顶点坐标为(-20,1).
(1)钢缆的最低点到桥面的距离是1米.
(2)两条钢缆最低点之间的距离是2×20=40米.
(3)是用配方法求得顶点坐标得到的,也可以直接代入顶点坐标公式中求得.
[师]从上面的例题我们可知,抛物线在现实生活中的应用很广,因此大家要学好并运用好它,对于给出的问题要认真思考,把实际问题转化为数学问题,从而用数学知识解决实际问题.
在上面的问题中,大家能否求出右面的抛物线的表达式呢?请互相交流.
解:因为左右两条抛物线是关于y轴对称的,而关于y轴对称的图形的特点是,所有的对应点的坐标满足横坐标是互为相反数,纵坐标相等,我们可以利用这个特点,在原有的左面的抛物线的表达式的基础上,得到右面抛物线的表达式,即把y不变,x换为-x代入y=0.0225x2+0.9x+10中,得
y=0.0225(-x)2+0.9(-x)+10
 =0.0225x2-0.9x+10.
=0.0225x2-0.9x+10.
[师]前几节课我们研究了不同形式的二次函数的图象,形如y=ax2,y=ax2+c,y=a(x-h)2,y=a(x-h)2+k.并对它们的性质进行了比较.但对于二次函数的一般形式y=ax2+bx+c(a、b、c是常数,a≠0),它是属于上面形式中的哪一种呢?还是另外一种,它的对称轴和顶点坐标是什么呢?下面我们一起来讨论这个问题.
投影片:(§2.4.2 A)
例:求二次函数y=ax2+bx+c的对称轴和顶点坐标.
解:把y=ax2+bx+c的右边配方,得
y=ax2+bx+c
=a(x2+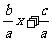 )
)
=a[x2+2·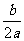 x+(
x+(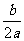 )2+
)2+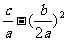 ]
]
=a(x+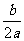 )2+
)2+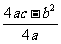 .
.
[师]大家看配方以后的形式属于前面我们讨论过的哪一种形式呢?
[生]属于y=a(x-h)2+k的形式.
[师]在y=a(x-h)2+k的形式中,我们知道对称轴为x=h顶点坐标为(h,k).对比一下,y=ax2+bx+c中的对称轴和顶点坐标是什么呢?
[生甲]对称轴是x= 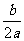 ,顶点坐标是(
,顶点坐标是(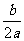 ,
,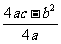 ).
).
[师]确定吗?大家再讨论一下.
[生]在y=a(x-h)2+k中是x-h,而y=a (x+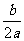 )2+
)2+ 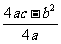 中是x+
中是x+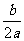 ,它们的符号不同,应把y=a(x+
,它们的符号不同,应把y=a(x+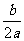 )2+
)2+
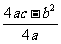 .进行变形得 y=a[x-(-
.进行变形得 y=a[x-(-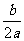 )2]+
)2]+ 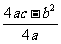 .再对照y=a(x-h)2+k的形式得对称轴为x=-
.再对照y=a(x-h)2+k的形式得对称轴为x=-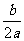 ,顶点燃坐标为(-
,顶点燃坐标为(-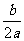 ,
,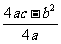 )
)
[师]这位同学回答得非常棒.
至此,所有的二次函数的形式我们就都讨论过了.
下面我们来研究一些实际问题.
(三)情感与价值观要求
1.经历将一些实际问题抽象为数学问题的过程,掌握数学的基础知识和基本技能,并能解决简单的问题.
2.初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点
运用二次函数的对称轴和顶点坐标公式解决实际问题.
教学难点
把数学问题与实际问题相联系的过程.
教学方法
讲解法.
教具准备
投影片三张
第一张:(记作§2.4.2 A)
第二张:(记作§2.4.2 B)
第三张:(记作§2.4.2 C)
教学过程
Ⅰ.创设问题情境,引入新课
[师]上节课我们主要讨论了相关函数y=ax2,y=a(x-h)2,y=a(x-h)‑+k的图象的有关性质,特别练习了求函数的对称轴和顶点坐标.我们知道学习的目的就是为了应用,那么究竟有什么用处呢?本节课将学习有关二次函数的应用.
Ⅱ.新课讲解
(二)能力训练要求
1.通过解决实际问题,让学生训练把教学知识运用于实践的能力.
2.通过学生合作交流来解决问题,培养学生的合作交流能力.
(一)教学知识点
1.体会建立二次函数对称轴和顶点坐标公式的必要性.
2.能够利用二次函数的对称轴和顶点坐标公式解决问题.
备课资料
参考练习
在同一直角坐标系内作出函数y=-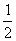 x2,y=-
x2,y=-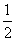 x2-1,y=-
x2-1,y=-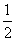 (x+1)2-1的图象,并讨论它们的性质与位置关系.
(x+1)2-1的图象,并讨论它们的性质与位置关系.
解:图象略
它们都是抛物线,且开口方向都向下;对称轴分别为y轴y轴,直线x=-1;顶点坐标分别为(0,0),(0,-1),(-1,-1).
y=-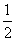 x2的图象向下移动1个单位得到y=-
x2的图象向下移动1个单位得到y=-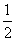 x2-1 的图象;y=-
x2-1 的图象;y=-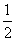 x2的图象向左移动1个单位,向下移动1个单位,得到y=-
x2的图象向左移动1个单位,向下移动1个单位,得到y=-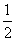 (x+1)2-1的图象.
(x+1)2-1的图象.
第2课时
课 题
§2.4.2 二次函数y=ax2+bx+c的图象(二)
教学目标
2.补充练习
1.随堂练习
4.议一议(投影片§2.4.1 D)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com