
2. 教学难点:
①一元二次方程的根与二次三项式因式分解的关系;一个二次三项式在实数范围内因式分解的条件。
②在列一元二次方程的方法解应用题时,分析题意找等量关系是难点;注意求解后,检验根是否符合实际意义。
[典型例题]
例1. 分解因式
①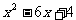 ②
②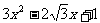
③ ④
④
⑤
分析:前四个均为二次三项式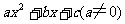 或二元二次三项式
或二元二次三项式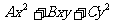 的因式分解,直接用公式进行分解。
的因式分解,直接用公式进行分解。
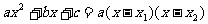 其中
其中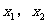 为方程
为方程 的两根。
的两根。
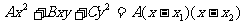 ,其中
,其中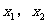 为关于x的方程
为关于x的方程 的两根。
的两根。
第五个用平方差公式,再用公式法分解二次三项式。
解:①令
∴
②解法1:令 ,则
,则
∴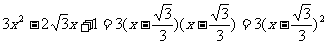
解法2:

解法3:

③令 ,解这个关于x的方程得:
,解这个关于x的方程得:

∴
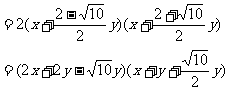
④∵
∴ 不能因式分解,在实数范围。
不能因式分解,在实数范围。
⑤
∵令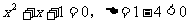 ,无实根。
,无实根。
∴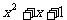 在实数范围内不能分解因式。
在实数范围内不能分解因式。
∵令
∴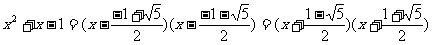
∴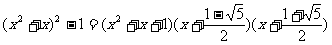
点拨:②中三种方法各有千秋,公式法,配方法,十字相乘法,注意结果写成幂的形式。③二元时选其中一元为主元,另一元为已知数,即可。注意最终结果的简洁形式,④⑤中都要考虑二次三项式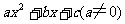 可在实数范围内因式分解的条件是:
可在实数范围内因式分解的条件是: ,⑤要综合应用,并注意因式分解必须彻底。
,⑤要综合应用,并注意因式分解必须彻底。
例2. 分解因式: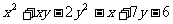
分析:形如 的多项式,叫关于x,y的二元二次多项式,它的因式分解有三种方法:①双十字相乘法,②待定系数法,③公式法。
的多项式,叫关于x,y的二元二次多项式,它的因式分解有三种方法:①双十字相乘法,②待定系数法,③公式法。
解:解法1:
∵
∴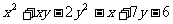
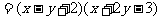
解法2:设
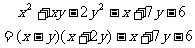

比较对应项系数
∴
解法3:整理为关于x的二次三项式
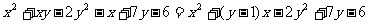
令 ,则
,则
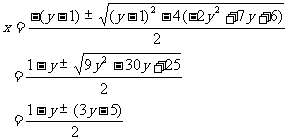
∴
∴
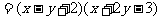
例3. 黄岗百货商店服装柜销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为迎接“六·一”,商场决定降价,扩大销售量,增加盈利,减少库存。经市场调查发现:如果每件童装每降价4元,那么每天平均可多售8件,要想每天平均在销售这种童装上盈利1200元,那么每件童装应降价多少元?
分析:经济类问题应用。要切实理解减少库存是本题需要。
解:设每件童装应降价x元,根据题意,


解得:
因要减少库存,∴ ,
,
答:每件童装应降价20元。
例4. 某中学的校办工厂的年产值1998年是50万元,年年增加,到2000年达60.5万元。问(1)平均每年的年产值增长率是多少?(2)三年总产值多少?
分析:储蓄中复利计本利和与生产值增长率问题。假设年利率为x,本金a,则n年后本利和为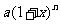 ,增长率亦如此。
,增长率亦如此。
解:(1)设每年平均增长率x,则1999年产值 万元,2000年产值
万元,2000年产值 万元,
万元,
由题意: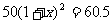

解得: (不合题意,舍去)
(不合题意,舍去)
答:平均每年增长率为10%。
(2)
答:1998至2000年这三年总产值为165.5万元。
点拨:注意舍去不合题意的根,别忽略(2)的计算与做答。
例5. 两个连续偶数积为288,求这两个数。
分析:两个连续偶数差2,可设x, 。
。
解:设这两个偶数分别为x,x+2,根据题意,
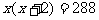
解得:

答:这两个连续偶数是16,18或-18,-16。
点拨:如果两个连续奇数也可这样设,但更好的设法是:
 ,就有
,就有
∴ 更简单。
更简单。
例6. 一个矩形的硬纸片,它的长比宽的2倍少4厘米,在它的四个角上各剪去一个边长为2厘米的正方形,然后折成一个无底的小盒子,如果这个小盒的体积为484立方厘米,求原来矩形纸片的长和宽。
分析:设原矩形宽为x厘米,那么长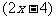 厘米,在四个角各剪去一个边长为2厘米的正方形折成无盖小盒,则小盒底面宽为
厘米,在四个角各剪去一个边长为2厘米的正方形折成无盖小盒,则小盒底面宽为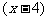 厘米,长为
厘米,长为 厘米,高为2厘米。
厘米,高为2厘米。
解:设原矩形纸片的宽为x厘米,则长为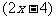 厘米,根据题意列方程,得:
厘米,根据题意列方程,得:

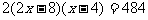
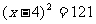
∴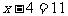 (负值舍去)
(负值舍去)
∴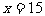

答:原矩形纸片的长为26厘米,宽为15厘米。
点拨:列一元二次方程可解决体面积有关的应用题,注意舍根。
例7. 一个直角三角形,斜边 ,两条直角边长相差
,两条直角边长相差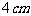 ,求这个直角三角形的两条直角边的长。
,求这个直角三角形的两条直角边的长。
分析:在Rt△中,三边a,b,c满足 ,这是构造方程的相等关系。
,这是构造方程的相等关系。
解:设一条直角边长为x cm,则另一条边长为 。
。
根据题意列方程 
解得  (不合题意,舍去)
(不合题意,舍去)
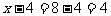 。
。
答:两条直角边长分别是8cm和4cm。
点拨:很多几何题求边时,用方程思想解决,而相等关系多由勾股定理提供,掌握本题很重要,体现了“几何问题代数化”。
例8. 用100cm的金属丝,作成矩形的框子,使面积分别为(1)500cm2;(2)625cm2;(3)800cm2。是否办得到,求出它的长和宽(精确到mm)。
分析:可列方程组解决面积问题。
解:设矩形长为x(cm),宽为y(cm),则
(1)
由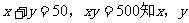 为方程
为方程 的两根。
的两根。

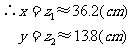
答:面积为500cm2时,长约是36.2cm,宽约是13.8cm。
(2)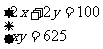
易知x,y是方程 的两根,
的两根,
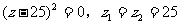
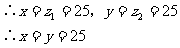
答:面积为625cm2时,长是25cm,宽也是25cm,围成边长25cm的正方形。
(3)
x,y为方程 的两根,
的两根,
 无实根。
无实根。
答:面积800cm2,周长100cm的矩形不存在。
点拨:解题后,思考三小题:用100cm长的铁丝围成500cm2的矩形做成了;再围大点,面积625cm2,围成了正方形;再大点,面积800cm2,围不成。长度有限的铁丝怎能围出要多大,有多大的矩形呢!当正方形时面积达到最大值。
[总结扩展]
(1)用公式法将二次三项式 因式分解的步骤是先求出方程
因式分解的步骤是先求出方程 的两个根,再将
的两个根,再将 形式。
形式。
(2)二次三项式 因式分解的条件是:当
因式分解的条件是:当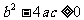 ,二次三项式
,二次三项式 在实数范围内可以分解;
在实数范围内可以分解; 时,二次三项式
时,二次三项式 在实数范围内不可以分解。
在实数范围内不可以分解。
(3)联系所学知识总结出遇见二次三项式因式分解的步骤:①首先考虑能否提取公因式;②其次考虑能否选用十字相乘法;③最后考虑公式法。
(4)通过二次三项式因式分解的学习,提高分析问题、解决问题的能力;通过结论探索、发现、推导、产生的过程,培养学生的探索精神,激发学生的求知欲望,对学生进行辩证唯物主义思想教育,渗透认识事物的一般规律。
(5)注意:①在进行类似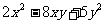 分解因式时,千万不要漏掉字母y;②因式分解一定进行到不能再分解为止;③分解时注意二次三项式
分解因式时,千万不要漏掉字母y;②因式分解一定进行到不能再分解为止;③分解时注意二次三项式 因式分解的条件。
因式分解的条件。
(6)“一元二次方程的应用”是“一元一次方程的应用”的继续和发展。由于用一元一次方程(或一次方程组)解的应用题,一般都可以用算术方法解,而用一元二次方程来解的应用题,一般说是不能用算术法来解的。所以,通过学习大家要认识到用代数方法解应用题的优越性和必要性。
(7)列方程解应用题的方法来说,列出一元二次方程解应用题与列出一元一次方程解应用题类似,都是根据问题中的相等关系列出方程,解方程,判断根是否适合题意,作出正确的答案。列出一元二次方程,其应用相当广泛,如在几何、物理及其他学科中都有大量问题存在。
(8)善于将实际问题转化为数学问题,严格审题,弄清各数据相互关系,正确布列方程。由此培养学生用数学的意识,渗透转化与方程的思想方法。
(9)进一步体会数字在实践中的应用,培养学生分析问题、解决问题的能力。
[模拟试题](答题时间:30分钟)
1. 教学重点:
①应用公式法将二次三项式因式分解;会用列一元二次方程的方法解决实际应用的问题。
②在列一元二次方程的方法解应用题时,分析题意找出表示全部含义的相等关系,是能否列出方程的前提和保证。
4. 通过一元二次方程的应用的学习,提高化实际问题为数学问题的能力和分析问题,解决问题的能力,培养用数学的意识;深刻体会转化,方程,数形结合等初等数学的思想方法。
3. 通过二次三项式的因式分解的学习,提高分析问题,解决问题的能力;进一步了解认识问题和解决问题的一般规律,即由一般到特殊,再由特殊到一般。
2. 学会用列一元二次方程的方法解实际应用题。
二次三项式的因式分解(用公式法)及一元二次方程的应用
[学习目标]
1. 熟练掌握二次三项式的意义;了解二次三项式的因式分解与解一元二次方程的关系;运用一元二次方程的求根公式在实数范围内将二次三项式分解因式。
备课资料(略)
3.补充例题(投影片§2.4.2 C)
2.有关桥梁问题(投影片§2.4.2 B)
2.补充练习
确定下列抛物线的开口方向、对称轴与顶点坐标.
(1)y=-x2+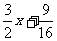 ;
;
(2)y= x2-
x2-
解:(1)y=-x2+ 
=-(x2- )
)
=-( x2- )
)
=-(x- )2+
)2+ .
.
开口方向向下,对称轴为x= ,顶点坐标为(
,顶点坐标为( ,
, ).
).
(2)y= x2-
x2-
= (x2-x-30)
(x2-x-30)
= (x2-x+
(x2-x+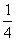 -
-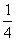 -30)
-30)
= (x-
(x-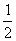 )2-
)2- .
.
开口方向向上,对称轴是x=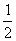 ,顶点坐标为(
,顶点坐标为(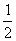 ,
, ).
).
Ⅳ.课时小节
本节课学习了如何用配方法把二次函数的一般形式化成顶点式,并能根据顶点式解决一些问题.
Ⅴ.课后作业
习题2.5
Ⅵ.活动与探究
利用Z+Z智能教育平台(新世纪版)研究二次函数的图象.
利用Z+Z智能教育平台(新世纪版)可以探索二次函数y=ax2+bx+c的系数(a,b,c与图象变化之间的关系.
先考察二次函数y=ax2的系数a对图象的影响.
利用Z十Z智能教育平台(新世纪版)在计算机上作出二次函数y=ax2的图象.其中系数a可以通过鼠标拖动y轴上标识为a的点而变化.图1和图2是a取不同值时得到的两个图象:

板书设计
§2.4.2 二次函数y=ax2+bx+c的图象(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com