
2、倒数和相反数是两个重要的概念,你能说出两者的区别吗?
(1) 若a,b互为相反数,则a+b= ,a,b的符号 ;
(2) 若a,b互为倒数,则a·b= ,a,b的符号 。
应用拓展:
基础演练
1. 结合“自主探究”中“试一试”,体会一下你是如何利用乘法的交换律、结合律和分配律来简化有理数的乘法运算的?把你的做法和同学们交流一下。
4、 做一做:
(1)8×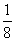 = ; (2)(-4)×(-
= ; (2)(-4)×(-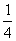 )= ;
(3)(-
)= ;
(3)(-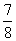 )×(-
)×(-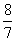 )= ;
)= ;
回顾反思:
3、 试一试:
(1)(-2.5)×(-3.1)×4;
(2)(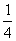 +
+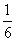 -
-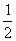 )×12;
)×12;
(3)4.98×(-5);
(4)9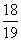 ×15;
×15;
2、 说出下面每一步计算的依据,并体会这样做的优越性:
(-0.4)×(-0.8)×(-1.25)×2.5
=-0.4×0.8×1.25×2.5 ……………… ( )
=-0.4×2.5×0.8×1.25 ……………… ( )
=-(0.4×2.5) ×(0.8×1.25) ……………… ( )
=-1×1
=-1
1、 仔细观察“情境”中三组题,你能发现什么结论?这些结论是否具有一般性?再用一些具体的数验证一下,并把它写成“一般式”。
2.5有理数的乘法与除法
情境问题:
填一填:
(1)5×(-6)= ; (-6)×5= 。
(2)[3×(-4)]×(-5)= ; 3×[(-4)×(-5)]= 。
(3)5×[3+(-7)]= ; 5×3+5×(-7)= 。
自主探究:
2.5 有理数的乘法与除法(一)
|
题目 |
2.5 有理数的乘法与除法(一) |
|
|
教学目标 |
掌握有理数的乘法运算规则 |
|
|
重点 |
感受有理数乘法的合理性; 能用法则进行有理数乘法运算 |
|
|
难点 |
从生活中的实例感受有理数的乘法 |
|
|
教学内容 |
教师活动 |
学生活动 |
|
一 引入情景 水文观测 (1) 如果水位每天上升4cm,那么3天后水位比今天高还是低?高(或低)多少? (2) 如果水位每天上升4cm,那么3天前水位比今天高还是低?高(或低)多少? (3) 如果水位每天下降4cm,那么3天后水位比今天高还是低?高(或低)多少? (4) 如果水位每天下降4cm,那么3天前水位比今天高还是低?高(或低)多少? 介绍我国是一个多水灾的国家,说明水文观测的重要性.请同学以防汛总指挥身份对水位进行预测和判断. (1) 水位上升记为+4,三天后记为+3,三天后水位变化是(+4)×(+3),也可以表示为4+4+4=12,即(+4)×(+3)=12,所以三天后水位变化是+12 (2) 水位上升记为+4,三天前记为-3,三天后水位变化是(+4)×(-3),也可以表示为一天前水位变化是-4, 两天前水位变化是-8, 三天前水位变化是-12,即(+4)×(-3)=-12,所以三天后水位变化是-12 (3) 水位下降记为-4,三天后记为+3,三天后水位变化是(-4)×(+3),也可以表示为(-4)+(-4)+(-4)=-12,即(-4)×(+3)=-12,所以三天后水位变化是-12 (4) 水位下降记为-4,三天前记为-3,三天后水位变化是(-4)×(-3),也可以表示为一天前水位变化是4, 两天前水位变化是8, 三天前水位变化是12,即(-4)×(-3)=12,所以三天后水位变化是-12 想一想:用上面的方法表示一天后两天后水位变化的式子,在书上表中填空. 讨论: 归纳乘法法则 两数相乘,同号得正,异号的负,并把绝对值相乘 任何数与0相乘都得0 例1(1)9×6=54 (2)(-9)×6=-54 (3)3×(-4)=-12 (4)(-3)×(-4)=12 练习(-7)×3=-21 ( 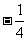 )×8=2 )×8=2(-48)×(-3)=144 (-3)×(-5)=15 (-6.5)×(-7.2)=46.8 100×0=0 ( 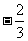 )×9=-6 )×9=-6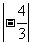 ×6=8 ×6=8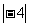 × ×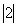 =8 =8作业:P50 1,6 |
口答 总结 朗读 自己练习 |
|
|
板书设计 |
|
5.小结
立方根和平方根有何异同?
比如,不同点:任何数都有立方根,正数和0有平方根,负数没有平方根;正数有两个平方根,任何数都有惟一的立方根;立方根等于本身的数有0、1、-1,平方根等于本身的数只有0.共同点:0的立方根和平方根都是0.
4.思维拓展
“讨论”和习题2.4第2题都是思维拓展的材料.教学中应较多地关注学生在解决问题中不同的思维策略.学生在解决问题过程中可能会表现出以下的不同水平:
(1)依据立方根的定义求解;
(2)从开立方与立方互为逆运算的角度求解;
(3)能从一类具体的例子的求解中归纳概括出一般形式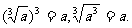
教师要尊重学生解决问题中表现出的不同水平,本节课思维拓展的主要目标是使学生不断获得解决问题的经验,提高思维水平,而不是从具体的例子中概括出公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com