
有理数的乘法这一节是学生刚开始经历有理数运算,是学生从现实世界和实例抽象出的过程,在具体的题目中探索有理数乘法运算的一些规律,培养学生观察与概括能力,培养学生今后学习代数的兴趣。
这节课的学习我们经历了一个“体验”、“领悟”、“概括”、“应用”的过程,主要学习了有理数的乘法法则.你在这个学习的过程中,有哪些感受?有何收获?掌握了什么?
[作业] P49习题2.5 题1
4.直接说出下列各题的运算结果.
①(-1)×(-2); ②3×5;
③3×(-4); ④(-5)×2;
⑤0×(-7); ⑥(-3)×(-2);
⑦(-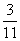 )×
)× ; ⑧(-
; ⑧(- )×0;
)×0;
⑨(-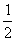 )×(-2); ⑩
)×(-2); ⑩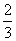 ×(-
×(-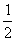 ).
).
3.计算.[生板演(谁想到黑板上板演),师指导评改(谁愿意当裁判)]
①(-7)×3; ②(-48)×(-3);
③(-6.5)×(-7.2); ④(-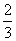 )×9.
)×9.
2.计算.[引导学生口述解答(谁愿意起来口述过程),师板书,强调先确定积的符号,再算绝对值]
(1)9×6; (2)(-9)×6;
(3)3×(-4); (4)(-3)×(-4).
师:同学们我们已经历经了实际问题--数学表示--法则概括的全过程,有了法则我们可以快速简捷解决两个有理数乘法运算(我们可以由算式直接运用法则来计算).下面就请同学们来解决以下问题:
1.确定下列两数积的符号.
①2×(-2.5); ②2×(+3);
③(-5)×(-7); ④(-4)×6;
⑤(-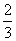 )×(-
)×(-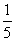 ); ⑥6×(
); ⑥6×(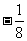 );
);
⑦(-5)×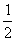 ; ⑧
; ⑧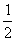 ×
×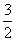 .
.
师:[演示课件(下表)]请同学们根据刚才所学及自己的经验,猜想表中各式的结果,并解释(+4)×(+2)=?与(-4)×(+1)=?的实际意义.请同学们前后四人一组,先小组讨论交流,并将讨论所得结果由组长记录在纸上,最后小组代表展示所得成果.[巡视指导,参与讨论交流]
|
(+4)×(+3)=+12, |
(-4)×(-3)=+12, |
|
(+4)×(+2)=
, |
(-4)×(-2)= , |
|
(+4)×(+1)= , |
(-4)×(-1)= , |
|
(+4)×0= , |
(-4)×0= , |
|
(+4)×(-1)= , |
(-4)×(+1)= , |
|
(+4)×(-2)= , |
(-4)×(+2)= , |
|
(+4)×(-3)=-12. |
(-4)×(+3)=-12. |
生:(+4)×(+2)=+8,实际意义表示每天买4个本子,2天后的本子比现在的本子多8个.
师:规定谁为正?
生:买本子记为正、几天后记为正、本子多记为正.
师:精彩!
生:(-4)×(+1)=-4,实际意义表示气温每天下降40C,1天后的气温比今天的气温低40C.
师:规定谁为正?谁为负?
生:气温下降记为负、几天后记为正、气温低记为负.
师:很形象!
师:仔细观察上表,你发现两个有理数相乘有规律可循吗?将你的发现先与同伴交流,之后再回答.
生:两个有理数相乘先确定积符号,再把绝对值相乘.
师:你认为如何确定积的符号?如何确定积的绝对值?
生:正正相乘得正,正负相乘得负,负正相乘得负,负负相乘得正.积的绝对值就等于这两个有理数绝对值的积.
师:两个有理数积的绝对值说得很好;积的符号也抓住了关键.有谁还想作一下补充吗?
生:与0相乘得0.
师:对!0既不是正数,也不是负数,应该考虑的.到此,我们已经把所有情形都考虑到了.能用简洁的语言概括这个规律吗?
[演示课件,并板书法则]
|
有理数的乘法(multiplication)法则 ①两数相乘,同号得正,异号得负,并把绝对值相乘. ②任何数与0相乘都得0. |
2.深入探究.
师:这些结果,是我们根据动画演示及实际生活经验获得的.那么同学们能不能把上述问题中的变化过程用数学式子来表达呢?其变化结果能用有理数来表示吗?我们若规定:水位上升记为正,水位下降记为负;几天后记为正,几天前记为负.
师:[探究问题1]按上面的规定,水位上升4cm记为“+4cm”,3天后记为“+3”,那么3天后的水位变化的数学式子是什么?
生:(+4)×(+3).
师:正确!你能说一说(+4)×(+3)的合理性吗?
生:水位每天上升4cm,按规定求3天后的水位应该用乘法,这样就是(+4)×(+3).
师:那么3天后的水位变化的结果呢?
生:由演示图可知,3天后的水位比今天高12cm,结果为+12cm.
师:你知道(+4)×(+3)与+12的关系吗?
生:我感到“水位上升4cm,3天后的水位变化的数学式子”应该与“3天后的水位变化的结果”相等,即(+4)×(+3)=+12.
师:回答得很好!这里实质上3天后的水位变化的过程与3天后的水位变化的结果应是一致的.
师:[探究问题2]按上面的规定,水位上升4cm记为“+4cm”,3天前记为“-3”,那么3天前的水位变化的数学式子是什么?
生:由问题1的解决,我想是(+4)×(-3).
师:这个发现了不起!将问题1的解决方法用在同一类型的问题解决.那么3天前的水位变化的结果呢?
生:由3天前的水位比今天低12cm可知,结果为-12cm.
师:你知道(+4)×(-3)与-12的关系吗?
生:相等,即(+4)×(-3)=-12.
[与上述探究过程相同,引导学生继续探究问题3与问题4,并结合下面图示,帮助学生理解,同时完成了下述表格,为进一步探究规律作准备]
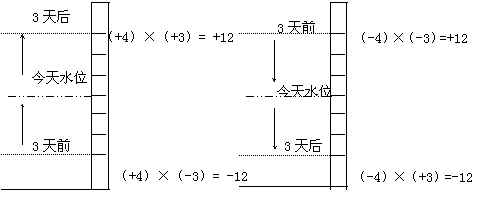
|
探 究 问 题 |
水位变化的数学式子表达 |
结果表示 |
|
1.水位上升4cm记为“+4”,3天后记为“+3”,则3天后的水位变化的 |
(+4)×(+3) = +12cm |
|
|
2.水位上升4cm记为“+4”,3天前记为“-3”,则3天前的水位变化的 |
(+4)×(-3) = -12cm |
|
|
3.水位下降4㎝记为“-4”,3天后记为“+3”,则3天后的水位变化的 |
(-4)×(+3) = -12㎝ |
|
|
4.水位下降4㎝记为“-4”,3天前记为“-3”,则3天前的水位变化的 |
(-4)×(-3) = +12cm |
1.初步感受.
问题1:如果水位每天上升4cm,那么3天后的水位比今天高还是低?高(或低)多少?[动画演示]
生:我觉得高了,因为以后3天水位都在上升.从动画演示看,高12cm.
师:很好!
问题2:如果水位每天上升4cm,那么3天前的水位与今天相比又如何呢?[动画演示]
生:因为3天前水位还没有升到今天的水位,所以3天前的水位比今天低.从演示看低12cm.
师:你真棒!
问题3:如果水位每天下降4cm,那么3天后的水位比今天高还是低?高(或低)多少?[动画演示].
生:低了,因为以后3天水位都在下降.从动画演示看,3天后的水位比今天低12cm.
师:你回答得真好!
问题4:如果水位每天下降4cm,那么3天前的水位比今天高还是低?高(或低)多少?[演示动画].
生:从演示中可以看出高了,我想水位每天下降4cm,3天前的水位还没有下降.高12cm.
师:太棒了!
师:同学们还记得1998年夏天长江发生的那一场特大洪水吧!你看,滚滚的急流使长江大堤有决堤的危险.当时啊,长江沿线,军民一心,严防死守,终于战胜了洪水,取得了抗洪的胜利.这其中,我们的水文工作日日夜夜、时时刻刻观察、记录着水位上升与下降的变化情况,为抗洪作出贡献.[配合导语,播放“长江洪水”影片,最后定格在水文站画面]
在这里,水文工作者遇到了水位上升与下降的问题.现在就让我们带着这个问题一起走进今天的数学乐园.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com