
3.计算:
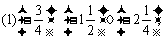


2.化简下列分数:

1.计算:
(1)(-42)÷12 ; (2)(-56)÷(-14); (3)-600÷15 ; (4)-18÷0.6;


师生共同归纳:本节课学习了有理数的倒数的意义,有理数的除法法则.在这过程中,同学们积极思维,通过多种途径,用自己的方式,从一些有理数除法的例子中,探究归纳出有理数的除法法则,收获很大,希望大家继续努力,争取更大的进步.
4.计算:
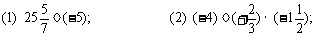

3.下列计算正确吗?为什么?
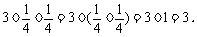
例1 计算:

解

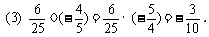


师:在上述解题的过程中,主要依据是什么?有什么好处呢?
生:根据除以一个数等于乘以这个数的倒数,可以把有理数的除法变成乘法.
教师总结:这里我们运用了一种常见的数学思想:转化思想!把不熟悉的除法转化成熟悉的乘法,这样有理数的乘除法就可以统一成乘法运算了.通过例1与练习,学生观察到商的符号与被除数、除数的符号存在一定的关系,从而总结出与乘法类似的法则:
两数相除,同号得正,异号得负,并把绝对值相除.零除以任何一个不等于零的数,都得零.
例2 化简下列分数:

解

师:除法运算与分数有什么关系呢?
生:除法运算与分数可以互化,所以可以利用除法化简分数,例2中除法也可以直接相除.
例3 计算:

解 
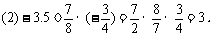
有理数的除法化成有理数的乘法以后,可以利用有理数的乘法的运算性质简化运算.乘除混合运算往往先将除法化为乘法,再确定积的符号,最后求出结果.
练习
1.计算:




根据上述问题,请学生讨论如何计算(-6)÷3?
生甲:根据常识, 可得出(-6)÷3= -2 .
生乙:我想到了小学时,我们把除法看成乘法的逆运算.因此,问题就变成求出一个数,使它与3的积等于-6 .
教师首先肯定两学生想法的准确性,并针对学生乙的想法作些说明,指出这种算法运用了有理数的除法,鼓励学生经常运用以前学过的知识,温故而知新.
教师板书:( ?)×3 = -6
答:∵(-2)×3= -6 ∴(-6)÷3= -2

师:三位同学各自用自己的方法求出了(-6)÷3,但结果是一致的. 现在请同学们看看,(*)式告诉我们什么?
组织学生交流讨论后,得出:除以3等于乘以3的倒数;有理数的除法可以转化为有理数的乘法来进行.
师:你能说出小学算术中的除法法则吗?
生:除以一个数等于乘以这个数的倒数.
师:小学里所指的数就是现在我们所说的正数,可如果这个数是有理数,我们如何求它的倒数呢?

生:积都是1.
有理数的倒数:乘积是1的两个数互为倒数(reciprocal).

想一想:0有没有倒数?
练习
写出下列各数的倒数: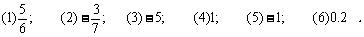
通过上述练习,现在你能说出如何求一个数的倒数吗?
总结:求一个数的倒数时,把这个数的分子分母颠倒后, 就求得这个数的倒数,0没有倒数.
(*)式告诉我们有理数的除法可以转化为有理数的乘法来进行.
做一做:
(1)8÷(-2)=8×( ) ; (2)6÷(-3)= 6×( );

问:根据(*)及上述四个填空,请大家展开想象的翅膀,大胆猜想.
答:有理数的除法同小学算术中除法一样,即除以一个数等于乘以这个数的倒数.
请学生自己编除法题验证该结论是否正确.
学生归纳:除以一个数等于乘以这个数的倒数. 注意:0不能作除数.
想一想:0为什么不能作除数?
我国北方某城市某年11月10日、11日、12日的平均气温分别是2℃、3℃、1℃,12月10日、11日、12日的平均气温分别是 -3℃、-1℃、-2℃.
问题1:该城市11月10日、11日、12日三日的平均气温是多少?
问题2:该城市12月10日、11日、12日三日的平均气温是多少?
对于问题1,学生很容易列出算式:(2+3+1)÷3=6÷3=2
得出:该城市11月10日、11日、12日三日的平均气温是2℃
对于问题2,引导学生列出算式:(-6)÷3,从而引出课题--有理数的除法.
2.5有理数的乘法和除法(2)
|
课 题 |
2.5有理数的乘法和除法2. |
课 型 |
新 授 课 |
|||
|
教 学 目 标 |
知识目标 |
1.掌握有理数乘法运算律,会运用乘法运算律进行有理数的乘法运算,特别是运用乘法运算律进行有理数乘法的简便运算; 2.掌握倒数的概念,会求非0有理数的倒数; |
||||
|
能力目标 |
3.进一步培养学生运用乘法运算律简化运算的能力; 4.使学生经历操作、观察、讨论、交流等活动,培养学生交流的能力; |
|||||
|
情感目标 |
5.通过学生的学习活动,不断学生养成良好的学习习惯,培养学生的探究、合作意识. |
|||||
|
教学重点 |
关注学生的合作交流;熟练运用乘法运算律进行有理数乘法的简便运算. |
|||||
|
教学难点 |
有理数的乘法乘法运算律运用. |
|||||
|
教学形式 |
小组讨论、师生合作. |
|||||
|
教具准备 |
多媒体 |
|||||
|
教 学 过
程 |
||||||
|
程序 |
教师活动 |
学生活动 |
设计意图 |
|||
|
一、 设境 引入 |
多媒体显示:“做一做” (一)计算: 1.(-6)×(-7),(-7)×(-6); 2×(-9),(-9)×2. 2.[2×(-3)]×(-4),2×[(-3)×(-4)]. 3.(-2)×[-3+5],(-2)×(-3)+(-2)×5. (二)计算: 1.8×  ;2.(-4)×(- ;2.(-4)×(- );3.(- );3.(-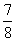 )×(- )×(-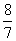 ). ). |
计算. 先括号内,后括号外. 先计算,再观察结果特征. |
由课本的“做一做”,用多媒体展示,引导学生在游戏中解决计算问题.这为研究运算律做好准备. 倒数的概念探究. |
|||
|
二、概括法则 |
(一)问题: 1.由刚刚的游戏与计算,你发现每一组算式的结果有什么特点?每一组算式又有什么特点?你能得到什么结论? 2.用文字语言与符号语言表示你所得到的结论. 要求:先小组讨论、交流,再派代表叙述所得结论. 参与小组讨论,指导叙述不完善的. (二)板书课题:有理数乘法和除法2 1.有理数乘法运算律(板书) 乘法交换律:ab=ba. 乘法结合律:(ab)c=a(bc). 乘法分配律:a(b+c)=ab+ac. 2.倒数(板书) 如果两个数的积为1,那么这两个数互为倒数 |
先讨论,再交流,后代表汇报所得结论. ①结果相同,这两个算式应该相等; ②小学里学习的乘法交换律、乘法结合律、乘法分配律在有理数范围内仍然成立; ③两个有理数相乘,交换加数的位置积不变;…… ④符号表述. ⑤联想小学倒数的概念,概括. |
让学生由自己的实际计算,观察算式的特点,通过讨论,发现结果,并用文字语言与符号语言加以表示等.这样,既将展示了运算律的形成过程,又让学生体验了合作学习,同时还提高了学生的数学表达能力. 感觉小学许多东西,在有理数范围内仍成立. |
|||
|
三、新知运用 |
(一)例题 计算: 1.4×(-8.99)×2.5; 2.(-5.76)× 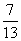 × ×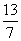 ; ;3.(  + +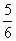 - - )×(-36). )×(-36).解: 1.4×(-8.99)×2.5 = (-8.99)×(4×2.5) = (-8.99)×10= -89.9; 2.(-5.76)× 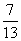 × ×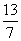 =(-5.76)×( 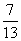 × ×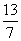 ) )=(-5.76)×1= -5.76; 3.(  + +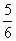 - - )×(-36) )×(-36)=  ×(-36)+ ×(-36)+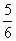 ×(-36)+(- ×(-36)+(- )×(-36) )×(-36)= -18-30+21 = -48+21 = -27. 引导反思:完成计算后,说说你运用运算律解决问题的感觉. 强调: 1.前两个计算题可以从前向后依次相乘,但这样麻烦,而利用乘法交换律、结合律简化计算; 2.第三题可以按运算顺序先求和,再相乘,发现烦琐后,不妨利用乘法分配律进行计算,这样较为方便. (二)练一练 1.计算: (1)  ×3; (2)(- ×3; (2)(- )×(- )×(-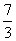 ); );(3)(-20)×(-  );(4)11×(- );(4)11×(-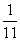 ). ).2.计算: (1)8×(-2)×(-5); (2)(-5)×10×(-2); (3)(-  - - + +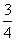 )×(-60); )×(-60);(4)3×5-(-5)×5+(-1)×5. 3.计算: (1)18×(- 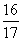 ); ); |
学生先独立完成,其中有三人板演,之后相互交流、评价,并对问题解决进行反思. 运用运算律解决这样的计算题,可以简化运算. 第一组4人先板演计算1; 注意:先确定积的符号,再算绝对值. 第二组6人,其中4人板演计算2;2人(优秀生)板演计算3. 注意:适当运用运算律简化运算. 全班交换批改,最后评价黑板板演题批改情况. |
1.重视双基教学. 例题(1、2是补充的)、练一练的设计,意在于让学生熟悉运算律的运用形成运用运算律简化运算的能力. 2.重视学生的合作交流. 例题的做、评价、反思,练一练的做、互批、评价,这些都为学生合作交流,搭建了一个良好的平台,重在提高学生合作交流能力. 3.重视优秀学生的能力提高. 练习3是补充的,为优秀学生灵活运用知识解决问题提供了很好的材料. |
|||
|
|
(2)(-11.5)×(-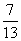 )+9.5×(- )+9.5×(-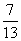 )-(-2)×(- )-(-2)×(-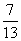 ). ).强调: 1.第2题中的(4)可以引导学生对两种方法进行讨论; 2.解题中出现的问题,要特别注意及时回授调节,以期真正彻底解决. |
法1:先求积再求和; 法2:逆用乘法分配律进行计算. |
4.解题中符号错误一定不会少,要注意不断强调,重点纠正. |
|||
|
四、回顾反思 |
你在这个学习的过程中有哪些收获?还有什么疑问? |
反思知识, 思想方法. |
培养学生反思自己思考与解决问题过程的意识,形成学生自主归纳和总结所学知识、方法的习惯与能力. |
|||
|
五、布置作业 |
P习题2.5 题2计算: (1)5×(-3)×(-9); (2)(-13)×(-15)×0×(-901); (3)(-3)×(-2)×(-4)×(-1); (4)(-  )× )×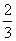 ×(- ×(-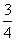 )×(- )×(- ); );题3计算: (1)0.1×(-0.001)×(-10); (2)0.125×(-2)×(-8); (3)( 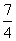 - -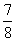 - - )×(- )×(-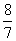 ); );(4)(-5)×7+13×7. 题8应用题(略). |
|
题3主要训练学生运用运算律简化运算的能力. 题8列式计算. |
|||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com