
2.掌握有理数的除法运算,考试中与其他运算综合在一起,经常出现.
例 (1)-5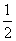 的倒数为_______,0.25的倒数为_______;
的倒数为_______,0.25的倒数为_______;
(2)若一个数的倒数为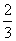 ,则此数的相反数为_______;
,则此数的相反数为_______;
(3)(-84)÷(-6)=_______,3÷(-8)=________;
(4)0÷(8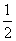 )=______,-5÷(-2
)=______,-5÷(-2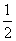 )=________.
)=________.
[解析] 求小数的倒数,要把小数化成分数;求带分数的倒数要将其分为假分数;有理数的除法,在整除情况下,直接相除,否则就把它转化为乘法进行计算.
答案是:(1)-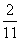 4 (2)-
4 (2)-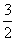 (3)14
-
(3)14
-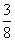 (4)0 2
(4)0 2
在线检测
1.会求一个数的倒数(0没有倒数).
3.倒数的性质:若a,b互为倒数,则ab=1.
思维点击
用除法法则进行除法运算的关键是:先确定商的符号,在整除的情况下,直接进行绝对值相除;在不能整除的情况下,特别是除数为分数时转化为乘法计算.
商的符号确定:根据有理数的除法法则及乘除统一成乘法后的有理数的乘法法则确定.
考点浏览
☆考点
2.有理数的除法法则
(1)除以一个数等于乘以这个数的倒数,0不能做除数.
(2)两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不为0的数是0.
1.倒数的概念:乘积是1的两个数互为倒数.
2.5.3 有理数的乘法与除法
知识平台
小明是这样做的:
因为 (-2)×7=-14,所以(-14)÷7=-2。
小丽是这样做的:
(-14)× =-2。
=-2。
小明和小丽的算法正确吗?他们这样做的依据是什么呢?
比较他们的算法:
(-14) ÷ 7 = -2
除号变成乘号 ↓ 7变成了它的倒数
(-14) ×  = -2
= -2

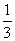 (4)-6÷ =-6×
(4)-6÷ =-6×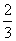 ;
; 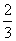 的倒数是 ; (3)0.1的倒数是 ;
的倒数是 ; (3)0.1的倒数是 ;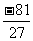 = ;(2)
= ;(2)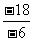 = ;
= ;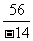 = ;(4)
= ;(4)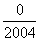 = ;
= ; |
教师活动内容、方式 |
学生活动方式 |
设计意图 |
|
例5 计算: (1)( 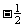 )÷( )÷(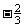 ) )(2)(-81)÷ 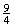 × ×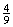 ÷(-16) ÷(-16)四、课堂小结: 本节课你的收获是什么? (有理数除法的两个运算法则) 五、作业: 见作业纸 |
学生板演,注意运算顺序 学生尝试小结,其他学生给予补充 |
培养学生综合能力与运算能力 |
2.5 有理数的乘法与除法(三)
|
题目 |
2.5 有理数的乘法与除法(三) |
||||||||||||||||||||
|
教学目标 |
掌握有理数的除法 |
||||||||||||||||||||
|
重点 |
有理数除法的运算法则 |
||||||||||||||||||||
|
难点 |
生活实际问题用有理数除法解决 |
||||||||||||||||||||
|
教学内容 |
教师活动 |
学生活动 |
|||||||||||||||||||
|
一 复习提问 有理数乘法法则 有理数乘法运算律 倒数的定义 二 新课引入 某足球队教练对球队防守能力进行分析,九场比赛失球数如下:
要求平均每场失球数以便进行纵向或横向的对比 解:[(-2)+(-4)+(-3)+(-1)+(0)+(-5)+(-1)+(-2)+(0)]÷9 =(-18)÷9 因为 (-2)×9=-18 且除法是乘法的逆运算 所以 (-18)÷9=-2 因为除以一个数等于乘以这个数的倒数 所以 (-18)÷9=(-18)× 进一步验证:(-10)÷2=-5 24÷(-8)=-3 (-12)÷(-4)=3 归纳: 有理数除法法则:除以一个不为0的数,等于乘以这个数的倒数;0除以任何一个不为0的数都得0 说明:0不能做除数 两数相除,同号得正,异号得负,并把绝对值相除 例1 (1)36÷(-9)=-4 (2)(-48)÷(-6)=8 (3)(-32)÷4×(-8)=64 (4)17×(-6)÷(-5)= 例2 (- =(- = (-81)÷ =(-81)× =(-36) ×(- =1 练习: P 49 1,2,3 作业: P50 4,5,7 |
回答 考虑解决办法 自己验证 记忆 板演 |
||||||||||||||||||||
|
板书设计 |
|
2.5有理数的乘法和除法(3)
|
课 题 |
2.5有理数的乘法和除法3. |
课 型 |
新 授 课 |
||||||||||||||||
|
教 学 目 标 |
知识目标 |
1.掌握有理数除法法则,会运用法则进行两个有理数的除法运算; 2.经历有理数除法法则的探索过程,体验将除法转化为乘法的思想方法; |
|||||||||||||||||
|
能力目标 |
3.进一步培养学生有理数运算的能力; 4.使学生经历操作、观察、讨论、交流等活动,培养学生参与活动的能力; |
||||||||||||||||||
|
情感目标 |
5.通过学生的学习活动,不断学生养成良好的学习习惯,培养学生的探究、合作意识. |
||||||||||||||||||
|
教学重点 |
关注学生的合作交流;熟练运用除法法则进行有理数除法的运算. |
||||||||||||||||||
|
教学难点 |
有理数除法法则形成过程的探索,及除法法则的运用. |
||||||||||||||||||
|
教学形式 |
小组讨论、师生合作. |
||||||||||||||||||
|
教具准备 |
多媒体 |
||||||||||||||||||
|
教 学 过
程 |
|||||||||||||||||||
|
程序 |
教师活动 |
学生活动 |
设计意图 |
||||||||||||||||
|
一、 设境 引入 |
多媒体显示:问题 已知,上周每上午8时的气温记录如下:
求:上周上午8时的平均气温是多少? 如何计算:(-14)÷7. |
计算:[(-3)+(-2)+(-3)+0+(-2)+(-1)+(-3)]÷7=(-14)÷7. |
由课本的“引题”,用多媒体展示,引导学生通过列式计算,得出(-14)÷7,如何计算?从而让学生产生求知欲望. |
||||||||||||||||
|
二、引导 探究 |
多媒体显示:问题1“议一议”小明与小丽的两种算法. 小明根据“小学里,除法是乘法的逆运算”得解法为: 因为(-2)×7=-14, 所以(-14)÷7=-2. 小丽根据“小学里,除以一个数等于乘以这个数的倒数”得解法为: (-14)÷7=(-14)× 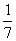 =-2. =-2.小明与小丽的算法正确吗?比较他们的算法你能得到什么? 结论:(-14)÷7=(-14)× 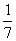 . .问题2“试一试”:下列各式中两数相除的商使多少?并用乘法验算: (1)(-10)÷2;(2)24÷(-8); (3)(-12)÷(-4);(4)0÷4;. (5)0÷(-12);(6)0÷(- 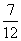 ) ) |
小组合作,讨论交流,展示结果. 正确;
号 变 成 了 乘 号 (-14)× 动手做. |
问题1展示两种算法,既使学生回顾小学时学习的内容,又为学生合作、讨论、交流提供了一个良好的素材,同时使学生经历了法则形成的过程,并在这一过程中体会道数学的方法. 问题2将上述探究的结论运用于计算,并进行检验,以初步感知它的正确性. |
||||||||||||||||
|
三、概括法则 |
(一)问题: 用文字语言与符号语言表示你所得到的结论. 要求:先小组讨论、交流,再派代表叙述所得结论. 参与小组讨论,指导叙述不完善的. (二)板书课题:有理数乘法和除法3 1.有理数除法法则(板书) 除以一个不等于0的数,等于乘以这个数的倒数. 0除以任何一个不等于0的数,都得0. 非零两数相除,同号得正,异号得负,并把绝对值相除. |
先讨论,再交流,后代表汇报所得结论. 符号表述:a÷b= 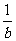 .(b≠0) .(b≠0)0÷a=0.(a≠0) 结合有理数的除法又有法则. |
问题讨论使学生体验了合作学习,同时还提高了学生的数学表达能力,特别是运用符号的表达数学表达能力. 板书法则,一让学生重视,二使学生便于运用. |
||||||||||||||||
|
三、新知运用 |
(一)例题 计算: (1)36÷(-9);(2)(-48)÷(-6); (3)(- 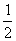 )÷(- )÷(-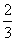 );(4)17×(-6)÷(-3). );(4)17×(-6)÷(-3).解:(板书示范) (1)36÷(-9)=-4; (2)(-48)÷(-6)=8; (3)(- 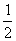 )÷(- )÷(-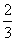 ) )=(- 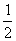 )×(- )×(-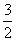 ) )= 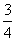 ; ;(4)17×(-6)÷(-3) =(-102)÷(-3) =34. 强调: 1.书写、符号及运算顺序等问题. 2.(4)的计算题可以从前向后依次进行. (二)练一练 1.求下列各数的倒数: (1)(-3);(2)(- 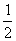 );(3) );(3)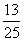 ;(4)(- ;(4)(-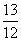 ). ).2.计算: (1)1÷(-5); (2)0÷(- 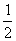 ); );(3)(-91)÷13; (4)(-63)÷(-9); (5)(- 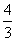 )÷(- )÷(-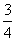 );(6)0.25÷(- );(6)0.25÷(-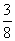 ). ). |
学生口述解答过程. 第一组4人口述答案; 第二组6人板演; |
1.重视双基教学. 例题、练一练的设计,意在于让学生熟悉除法法则的运用,提高运算的能力. 2.重视学生的主体. 例题的口述解答过程,练一练的做、互批、评价,这些都充分主体作用发挥提供了一个良好空间. 3.重视优秀学生的能力提高. 练习3是补充的,为优秀学生灵活运用知识解决问题提供了很好的材料. |
||||||||||||||||
|
|
3.计算: (1)12×(-3)÷(-4); (2)(-6)÷2×(- 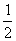 ); );(3)(-5)÷(-  )×5; )×5;(4)(-2)÷(-10)×(-3 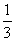 ). ).强调: 1.第3题按先后顺序进行; 2.解题中出现的问题,要特别注意及时回授调节,以期真正彻底解决. |
第三组4人,中等学生板演. 全班交换批改,最后评价黑板板演题批改情况. |
4.解题中符号错误一定不会少,要注意不断强调,重点纠正. |
||||||||||||||||
|
五、回顾反思 |
你在这个学习的过程中有哪些收获?还有什么疑问? |
反思知识, 思想方法. |
培养学生反思自己思考与解决问题过程的意识,形成学生自主归纳和总结所学知识、方法的习惯与能力. |
||||||||||||||||
|
五、布置作业 |
P习题2.5 题4计算: (1)(-20)÷10; (3)(-105)÷(-5); (5)(-25)÷  . .题5计算: (2)100÷ 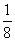 ×(-8); ×(-8);(4) 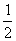 ×(- ×(- )÷ )÷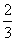 ; ;(6)(-48)÷  ÷(-12)× ÷(-12)× . .题10应用题(略). |
|
题4基本法则运用. 题5主要训练学生灵活运用法则,计算乘除混合运算的能力. 题10列式计算,尝试运用,提高运用能力. |
||||||||||||||||
2.5 有理数的乘法与除法(二)
|
题目 |
2.5 有理数的乘法与除法(二) |
|
|
教学目标 |
掌握有理数的乘法的运算律 并运用运算律简便计算 了解倒数 |
|
|
重点 |
有理数乘法的运算律 |
|
|
难点 |
适当使用运算律使计算简便 |
|
|
教学内容 |
教师活动 |
学生活动 |
|
一 复习提问 有理数乘法法则 二 新课引入 学生分别计算(-6)×(-7)=42 (-7)×(-6)=42 同样计算8×(-4)=-32 (-4)×8=-32 联系小学学过的乘法交换律,得出结论: 有理数乘法交换律: a×b=b×a 学生分别计算[(-3) ×(-5) ]×2=30 (-3) ×[(-5) ×2]=30 同样计算[2×(-4)] ×7=-56 2×[(-4)×7]=-56 联系小学学过的乘法结合律,得出结论: 有理数乘法结合律: (a×b) ×c=a×(b×c) 学生分别计算 (-4)×(-3+5)=(-4)×2=-8 (-4)×(-3)+(-4)×5=12-20=-8 同样计算 (-6)×( 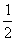 + +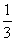 )=-5 )=-5(-6)× 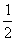 +(-6)× +(-6)×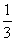 =-5 =-5联系小学学过的乘法分配律,得出结论: 有理数乘法分配律: a×(b+c)=a×b+a×c 强调指出,适当使用乘法运算律,可以使运算简便 例1 ( 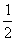 + +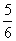 - -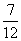 )×(-36) )×(-36)= 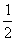 ×(-36)+ ×(-36)+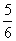 ×(-36)- ×(-36)-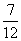 ×(-36) ×(-36)=-18+(-30)+21 =-27 例 2 8× 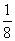 =1 =1(-4)×(- 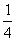 )=1 )=1(- 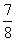 )×(- )×(-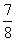 )=1 )=1定义:乘积为1的两个数,互为倒数 例 3 6×(-4)×  =(-4)×(6×  ) )=(-4) ×1 =-4 练习: P46 1,2 作业: P50 2,3 |
回答 记忆 记忆 记忆 记忆 板演 |
|
|
板书设计 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com