
1、黄金比的来历
如图,如果=,那么点C叫做线段AB的黄金分割点。

由=,得AC2=AB·CB
设AB=1, AC=x ,则CB=1-x
∴x2=1×(1-x) 即:x2+x-1=0
解这个方程,得
x1= , x2=(不合题意,舍去)
所以:黄金比=≈0.618
 注意:黄金比的准确数为,近似数为0.618.
注意:黄金比的准确数为,近似数为0.618.
上面我们应用一元二次方程解决了求黄金比的问题,其实,很多实际问题都可以应用一元二次方程来解决。
3、哪些一元二次方程可用分解因式法来求解?
(方程一边为零,另一边可分解为两个一次因式)
(1)x2+2x+1=0 (2)x2+x-1=0
2、什么叫黄金分割?黄金比是多少?(0.618)
其步骤为:审、设、列、解、验、答.
解:设每台冰箱的定价应为x元,根据题意,得
(x-2500)(8+4×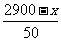 )=5000.
)=5000.
解这个方程,得
x1=x2=2750.
所以,每台冰箱的定价应为2750元.
2、列方程解应用题的关键是寻找等量关系。
1、列方程解应用题的步骤
(1)设未知数;(2)列方程;(3)解方程;(4)检验;(5)作答。
2、做一做:某商场将进货价为30元的台灯以40元售出,平均每月能售出600个,调查表明这种台灯的售价每上涨一元,某销售量就减少10个,为了实现平均每月20000的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
分析:每个台灯的销售利润×平均每天台灯的销售量=10000元
可设每个台灯涨价x元。
(40+x-30) ×(600-10x)=10000
答案为:x1=10, x2=40
10+40=50, 40+40=80
600-10×10=500 600-10×40=200
在日常生活生产中,我们常遇到一些实际问题,这些问题可用列一元二次方程的方法来解答。
1、讲解例题:
例2、新华商场销售某种冰箱,每台进货价为2500元,市场调研表明,为销售价为2900元时,平均每天能售出8台,而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价为多少元?
分析:
|
|
每天的销售量(台) |
每台的利润(元) |
总利润(元) |
|
降价前 |
8 |
400 |
3200 |
|
降价后 |
8+4× |
400-x |
(8+)×(400-x) |
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
如果设每台冰箱降价为x 元,那么每台冰箱的定价就是(2900-x)元,每台冰箱的销售利润为(2900-x-2500)元。这样就可以列出一个方程,进而解决问题了。
解:设每台冰箱降价x元,根据题意,得:
(2900-x-2500)(8+4×)=5000
解这个方程:
(400-x)(200+2x)=5000×25
-2x2+600x=125000-80000
x2-300x+22500=0
(x-150)(x-150)=0
解这个方程,得:
x1=x2=150
2900-150=2750 元
所以,每台冰箱应定价为2750元。
关键:找等量关系列方程。
4、销售利润= -
[销售价] [销售成本]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com