
24、21、16、9.
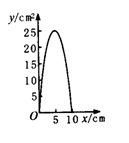
(3)图象如右图.
[师]大家可能注意到了函数的图象在第一象限.可是我们知道开口向下的抛物线可以到达第四象限和第三象限,这是什么原因呢?
[生]因为自变量的取值只取到了1至9,而这些点正好都在第一象限,所以图象只能画在第一象限.
[师]大家同意这种说法吗?
[生]不同意.不是因为列表中自变量的取值的原因,而是由于实际情况.函数值y是面积,而面积是不能为负值的.如果脱离了实际问题,单纯地画函数y=-x2+10x的图象,就不是在第一象限作图象了.
[师]非常棒.
投影片;(§2.5 A)
长方形的周长为20 cm,设它的一边长为xcm,面积为ycm2.y随x变化而变化的规律是什么?你能分别用函数表达式、表格和图象表示出来吗?
(1)用函数表达式表示:y= .
(2)用表格表示:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10-x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
(3)用图象表示:
[师]请大家互相交流.
[生](1)一边长为x cm,则另一边长为(10-x)cm,所以面积为:
 y=x(10-x)=-x2+10x
y=x(10-x)=-x2+10x
(2)表中第二行从左至
右依次填9、8、7、6、5、
4、3、2、1;第三行从左至
右依次填9、16、21、24、25、
4.小结
(1)怎样的数是无理数?请你举出几个无理数;
(2)说说你对数的认识.
3.例题教学
课本没有安排例题,教学时可以用练习第1题作为例题.
1.情境创设
在研究边长为1的正方形的对角线的长是多少的问题中,我们发现了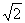 ,说说你对
,说说你对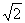 的认识,比如,用刻度尺度量,可知
的认识,比如,用刻度尺度量,可知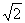 约等于1.4;在直角三角形中,斜边大于直角边,所以
约等于1.4;在直角三角形中,斜边大于直角边,所以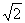 大于1;三角形中两边之和大于第三边,所以
大于1;三角形中两边之和大于第三边,所以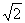 小于2;因为12=1, 22=4,(
小于2;因为12=1, 22=4,(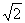 )2=2,所以1<
)2=2,所以1<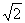 <2;因为1.52= 2.25,(
<2;因为1.52= 2.25,(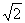 )2=2,所以
)2=2,所以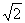 <1.5……引导学生尝试用已有的知识和经验,从不同的角度描述
<1.5……引导学生尝试用已有的知识和经验,从不同的角度描述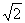 了,从中体会面对新问题的策略.
了,从中体会面对新问题的策略.
6.通过用不同的方法比较两个无理数的大小,理解估算的意义,发展数感和估算能力.
[教学过程(第一课时)]
5.经历用有理数估算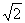 的探索过程,从中感受“逼近”的数学思想.
的探索过程,从中感受“逼近”的数学思想.
4.能利用计算器比较实数的大小、进行实数的四则运算.
3.了解有理数的运算在实数范围内仍然适用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com