
2.(1)你知道下面每一个图形中各有多少个圆圈吗?为什么?
(2)完成下表;

|
边上的小圆圈数 |
1 |
2 |
3 |
4 |
5 |
|
小圆圈的总数 |
|
|
|
|
|
(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么?
解:(1)第1个图形中有1个小圆圈.
第2个图形中有1+6=7个小圆圈.
第3个图形中有7+2×6=19个小圆圈.
第4个图形中有19+3×6=37个小圆圈.
(2)从左至右填1.7,19,37,61.
(3)m=6×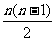 +1=3n2-3n+1.
+1=3n2-3n+1.
板书设计
§2.5 用三种方式表示二次函数
二次函数的三种表示方式有什么特点?它们之间有什么联系?与同伴进行交流.
[生]表格可以直观地找到对应点,图象就是把一对一对的对应点连接起来的,表达式反映出函数与自变量之间的关系.
它们之间的联系是:根据表达式可以求得一对一对的对应点,用光滑的曲线把对应点连接起来即为图象.
[师]很好.下面我们来更系统地学习它们各自的特点及联系.
投影片:(§2.5 D)
函数的表格表示可以清楚、直接地表示出变量之间的数值对应关系;函数的图象表示可以直观地表示出函数的变化过程和变化趋势;函数的表达式可以比较全面、完整、简洁地表示出变量之间的关系.这三种表示方式各自有各自的优点,它们服务于不同的需要.
它们的联系是三种方式可以互化,由表达式可转化为表格和图象表示,每一种方式都可转化为另两种方式表示.
Ⅲ:课堂练习
1.(1)你知道下面每一个图形中各有多少个小圆圈吗?第6个图形中应该有多少个小圆圈?为什么?

(2)完成下表:
|
边上的小圆圈数 |
1 |
2 |
3 |
4 |
5 |
|
小圆圈的总数 |
|
|
|
|
|
(3)如果用n表示等边三角形边上的小圆圈数,m表示这个三角形中小圆圈的总数,那么m和n的关系是什么?
解:(1)观察前5个图形可知,第2个图形比第1个多2个小圆圈,第3个比第2个多3个,第4个比第3个多4个,第5个比第4个多5个,据此第6个应比第5个多6个小圆圈,因此第6个图形应该有21个小圆圈.
(2)从左至右应填1,3,6.10,15.
(3)m=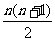 .
.
Ⅳ.课时小结
本节课我们经历了用三种方式表示变量之间二次函数关系的过程,体会了三种方式之间的联系与各自不同的特点.根据二次函数的不同表示方式,从不同的侧面对函数性质进行了研究.如最值问题和y随x的变化而变化等问题.
Ⅴ.课后作业
习题2.6
Ⅵ. 活动与探究
4.(1)因为数可以
是正数、负数和零,所
以x的取值范围为任何
实数.
(2)y=x2-2x=(x2-2x
+1)-1=(x-1)2-1.
因此图象的对称轴为x=1,顶点坐标为(1.-1).
(3)因为开口向上,对称轴x=1,所以在对称轴左侧.即x<1时,y的值随x值的增大而减小;在对称轴右侧,即x>1时,y的值随x值的增大而增大.
(4)通过观察图象可知.
3.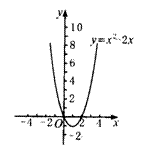 图象如右图.
图象如右图.
2.
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
15 |
8 |
3 |
0 |
-1 |
0 |
3 |
8 |
15 |
4.根据以上三种表示方式问答下列问题:
(1)白变量x的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述y随x的变化而变化的情况?
(4)你是分别通过哪种表示方式回答上面三个问题的?
[师]请大家互相交流.
[生]解:1.因为较大的一个数为x,那么较小的数为(x-2),则积y=x(x-2)=x2-2x所以函数的表达式为y=x2-2x.
3.用图象表示:
2.用表格表示:
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
投影片:(§2.5 C)
两个数相差2,设其中较大的一个数为x,那么它们的积y是如何随x的变化而变化的?你能分别用函数表示式、表格和图象表示这种变化吗?
1.用函数表达式表示:y= .
投影片:(§2.5 B)
(1)在上述问题中,自变量x的取值范围是什么?
(2)当x取何值时,长方形的面积最大?它的最大面积是多少?你是怎样得到的?请你描述一下y随x的变化而变化的情况.
[师]自变量x的取值范围即是使函数有意义的自变量的取值范围.请大家互相交流.
[生](1)因为x是边长,所以x应取正数,即x>0,又另一边长(10-x)也应大于0,即10-x>0,所以x<10,这两个条件应该同时满足,所以x的取值范围是0<x<10.
(2)当x取何值时,长方形的面积最大,就是求自变量取何值时,函数有最大值,所以要把二次函数y=-x2+10x化成顶点式.当x=-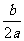 时,函数y有最大值
时,函数y有最大值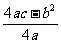 .
.
∴y=-x2+10x=-x2+10x=-(x2-10x)
=-(x2-10x+25-25)
=-(x-5)2+25.
∴当x=5时,长方形的面积最大,最大面积是25 cm2.
可以通过观察图象得知.
也可以代入顶点坐标公式中求得.
当x=-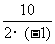 =5时,
=5时,
y最大=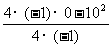 =25cm2.
=25cm2.
当x由1至5逐渐增大时,y的值逐渐增大,当x由5至10逐渐增大时,y的值逐渐减小。
[师]回答得棒极了.
这是一个实际问题,面积y为边长x的二次函数,求当x取何值时,长方形的面积最大.实际上就是求二次函数的最值,描述y随x的变化而变化的情况,就是以对称轴为分界线,一边为y随x的增大而减小,另一边是y随x的增大而增大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com