
4.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.若该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前七个月的利润总和与t之间的关系)为s=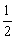 t2-2t.
t2-2t.
(1)第几个月末时,公司亏损最多?为什么?
(2)第几个月末时,公司累积利润可达30万元?
(3)求第8个月公司所获利润是多少万元?
3.某商场以80元/件的价格购进西服1000件,已知每件售价为100元时,可全部售出.如果定价每提高1%,则销售量就下降0.5%,问如何定价可使获利最大?(总利润=总收入-总成本).
2.某旅社有客房120间,每间房的日租金为50元时,每天都客满,旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
1.某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
2.6 何时获得最大利润 同步练习
2.6有理数的乘方第二课时
|
题目 |
2.6有理数的乘方2 |
|
|
教学目标 |
会用科学计数法表示较大的数 |
|
|
教学重点 |
用科学计数法表示较大的数 |
|
|
教学难点 |
较大的数转换成科学计数法表示的数 |
|
|
教学内容 |
教师活动 |
学生活动 |
|
一 复习提问 有理数乘方的定义 幂的定义 指数的定义 底数的定义 幂的正负 二 新课引入 光的传播速度大约为300 000 000m/s 声音的传播速度大约为430m/s(常温) 人体含有红细胞25 000 000 000 000 太阳系形成于距今4567000000 300000000 ×60× 60 ×24 ×365 米/ 年= 9 460 800 000 000 000米/ 年= 9 兆4608 亿公里 用计算器计算5 000 000×5 000 000 利用乘方我们可以表示一些较大的数 例如:300 000 000就是3×100 000 000结合上节课的练习也可以表示成3×10 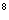 5 000 000×5 000 000=25 000 000 000 000就是2.5×10 000 000 000 000,也可以表示成2.5×10  一般的,一个大于10的数可以写成a×10 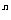 的形式,其中1<a<10,n是正数,这种计数法称为科学计数法 的形式,其中1<a<10,n是正数,这种计数法称为科学计数法例 1972粘3月发射的“先驱者10号”,是人类发往太阳系外的第一颗人造太空探测器,至2003年2月人们最后一次收到它发回的信号时,它已飞离地球12 200 000 000km,用科学计数法表示这个距离 解:12 200 000 000可表示成1.22×10  km km相关资料: 此前的一次联络是在1月22日,当时地面控制人员收到了从“先驱者10号”发回的响亮而清晰的信号。那时“先驱者10号”距离地球122亿公里,从飞船发回的信号用了11小时20分才到达地球先驱者10号”于1972年3月2日发射升空,原定考察计划只有21个月,但实际上它的“探测生命”之长,远远超出了人们的预期。直到1997年3月底,科学家才正式结束“先驱者10号”的科学考察使命,宣告它正式“退役”。在“服役”的25年间,“先驱者10号”在太空探索领域创造了一系列的“第一”。它第一个穿过小行星带成功到达木星附近,利用“近水楼台”的优势拍到了近距离特写图片;1983年,它又第一个飞出太阳系向金牛座飞去,但据估计,它至少还得再飞200万年,才能掠过与金牛座距离最近的恒星。在这之后,科学家仍不定期地与“先驱者10号”联系,并在此基础上试验了一些尖端通信技术。?? 先驱者10号”携带了一张镀金盘,上边刻有一封问候信和一张标明地球在太阳系中位置的地图 练习: P57 1,2,3 作业: P58 5,7 |
回答 尝试能否将这些数字输入计算器 尝试能否显示 |
2.6有理数的乘方
|
题目 |
2.6有理数的乘方 |
|
|
教学目标 |
1知道有理数乘方运算与有理数乘法运算之间的关系 2 知道底数,指数和幂的概念 3 会求有理数的正整数指数幂 |
|
|
教学重点 |
1有理数乘方运算与有理数乘法运算之间的关系 2底数,指数和幂的概念 |
|
|
教学难点 |
求有理数的正整数指数幂 |
|
|
教学内容 |
教师活动 |
学生活动 |
|
一 复习提问 有理数乘法的运算法则和运算律 二 新课引入 古代印度舍罕王重赏他的宰相--国际象棋的发明人达依乐的故事。达依乐只求国王在国际象棋的64个格中放入麦粒,各格的麦粒数依次是1,2,4,8,16,…,每格是前一格的2倍 拉面拉扣了6次有多少根面条? 用橡皮筋模拟 一张报纸可以对折几次? 折到不能再折时报纸有几层? 讨论: 生活中类似的实例 切菜,生物繁殖,传销… 2×2×2×2×2×2记为2 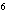 ,读作“2的6次方” ,读作“2的6次方”7×7记为7  ,读作“7的3次方” ,读作“7的3次方”一般地, 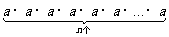 记为 记为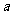 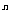 ,读作“ ,读作“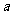 的n次方” 的n次方”定义: 求相同因数的积的运算叫做乘方,乘方运算的结果叫做幂. 2 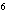 ,7 ,7 也可以看做是乘方运算的结果,这时它们表示的数读作“2的6次幂”,“7的3次幂” 也可以看做是乘方运算的结果,这时它们表示的数读作“2的6次幂”,“7的3次幂”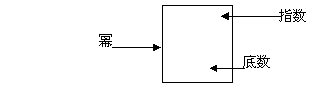 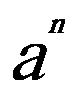 例1 计算: 2  =2×2×2×2×2×2=64 =2×2×2×2×2×2=647  =7×7×7=343 =7×7×7=343(-3) 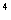 =(-3)×(-3)×(-3)×(-3)=81 =(-3)×(-3)×(-3)×(-3)=81(-4)  =(-4)×(-4)×(-4)=-64 =(-4)×(-4)×(-4)=-64例2 计算: ( 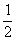 ) ) =( =(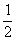 )×( )×(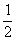 )×( )×(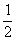 )×( )×(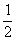 )×( )×(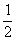 )=( )=(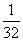 ) )( 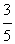 ) ) =( =(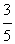 )×( )×(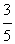 )×( )×(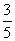 )=( )=(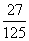 ) )(- 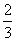 ) )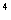 =(- =(-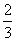 )×(- )×(-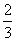 )×(- )×(-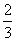 )×(- )×(-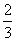 ) )=( 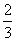 )×( )×(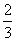 )×( )×(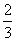 )×( )×(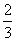 ) )= 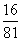 分析: 为什么说传销是骗人的,结合所学的知识加以解释 讨论: (-1)  , (-1) , (-1) 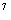 ,(- ,(-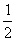 ) ) 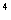 ,(- ,(-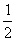 ) )  是正数还是负数? 是正数还是负数?负数幂的符号如何确定? 结论: 正数的任何次幂都是正数 负数的奇次幂是负数,负数的偶次幂是正数 特别的,一个数的二次方称为这个数的平方,一个数的三次方称为这个数的立方 练习:P56 1,2 作业:P58 1,2,3 |
回答 试验后回答 记忆 |
4、 “一般--特殊--一般”的数学思想方法是研究问题的一种常用方法。
3、 关注生活,用数学眼光观察生活中的实际问题。
2、 底数为负数和分数时候应加括号
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com