
3.议一议(投影片§2.6 B)
乙补充例题(投影片§2.6 C)
2.做一做
投影片:(§2.6 C)
已知--个矩形的周长是24 cm.
(1)写出这个矩形面积S与一边长a的函数关系式.
(2)画出这个函数的图象.
(3)当a长多少时,S最大?
[师]分析:还是有关二次函数的最值问题,所以应先列出二次函数关系式.
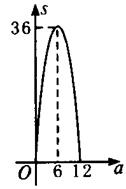
[生](1)S=a(12-a)=a2+12a=-(a2-12a+36-36)=-(a-6)2+36.
(2)图象如下:
(3)当a=6时,S最大=36.
Ⅲ.课堂练习
P61
解:设销售单价为;元,销售利润为y元,则
y=(x-20)[400-20(x-30)]
=-20x2+1400x-20000
=-20(x-35)2+4500.
所以当x=35元,即销售单价提高5元时,可在半月内获得最大利润4500元.
Ⅳ.课时小结
本节课经历了探索T恤衫销售中最大利润等问题的过程,体会了二次函数是一类最优化问题的数学模型,并感受了数学的应用价值.
学会了分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题中的最大(小)值,提高解决问题的能力.
Ⅴ.课后作业
习题2.7
Ⅵ.活动与探究
某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40-70元之间.市场调查发现:若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多销售3箱,价格每升高1元,平均每天少销售3箱.
(1)写出平均每天销售(y)箱与每箱售价x(元)之间的函数关系式.(注明范围)
(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式(每箱的利润=售价-进价).
(3)求出(2)中二次函数图象的顶点坐标,并求当x=40,70时W的值.在坐标系中画出函数图象的草图.
(4)由函数图象可以看出,当牛奶售价为多少时,平均每天的利润最大?最大利润为多少?
解:(1)当40≤x≤50时,则降价(50-x)元,则可多售出3(50-x),所以y=90+3(50-x)=-3x+240.当50<x≤70时,则升高(x-50)元,则可少售3(x-50)元,所以y=90-3(x-50)=-3x+240.
因此,当40≤x≤70时,y=-3x+240.
(2)当每箱售价为x元时,每箱利润为(x-40)元,平均每天的利润为W=(240-3x)(x-40)=-3x2+360x-9600.
(3)W=-3x2+360x-9600
=-3(x2-120x+3600-3600)-9600
=-3(x-60)2+1200.
所以此二次函数图象的顶点坐标为(60, 1200).
当x=40时,W=-3(40-60)2+1200=0;
当x=70时,W=-3(70-60)2+1200=900.
草图略.
(4)要求最大利润,也就是求函数的最大值,只要知道顶点坐标即可.
由(3)得,当x=60时,W最大=1200.
即当牛奶售价为每箱60元时,平均每天的利润最大,最大利润为1200元.
板书设计
§2.6 何时获得最大利润
(1)利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系.
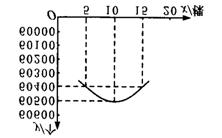
(2)增种多少棵橙子树,可以使橙子的总产量在60400个以上?
[生]图象如上图.
(1)当x<10时,橙子的总产量随增种橙子树的增加而增加;当x>10时,橙子的总产量随增种橙子树的增加而减小.
(2)由图可知,增种6棵、7棵、8棵、9棵、10棵、11棵、12棵、13棵或14棵,都可以使橙子总产量在60400个以上.
还记得本章一开始的“种多少棵橙子树”的问题吗?我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式y=(600-5x)(100+x)=-5x2+100x+60000.
我们还曾经利用列表的方法得到一个猜测,现在验证一下你的猜测是否正确?你是怎么做的?与同伴进行交流.
[生]因为表达式是二次函数,所以求橙子的总产量y的最大值即是求函数的最大值.
所以y=-5x2+100x+60000
=-5(x2-20x+100-100)+60000
=-5(x-10)2+60500.
当x=10时,y最大=60500.
[师]回忆一下我们前面的猜测正确吗?
[生]正确.
投影片:(§2.6 A)
某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.

请你帮助分析,销售单价是多少时,可以获利最多?
没销售单价为x(x≤13.5)元,那么
(1)销售量可以表示为 ;
(2)销售额可以表示为 ;
(3)所获利润可以表示为 ;
(4)当销售单价是 元时,可以获得最大利润,最大利润是 .
[师]从题目的内容来看好像是商家应考虑的问题:有关利润问题.不过,这也为我们以后就业做了准备,今天我们就不妨来做一回商家.从问题来看就是求最值问题,而最值问题是二次函数中的问题.因此我们应该先分析题意列出函数关系式.
获利就是指利润,总利润应为每件T恤衫的利润(售价一进价)乘以T恤衫的数量,设销售单价为x元,则降低了(13.5-x)元,每降低1元,可多售出200件,降低了(13.5-x)元,则可多售出200(13.5-x)件,因此共售出500+200(13.5-x)件,若所获利润用y(元)表示,则y=(x-2.5)[500+200(13.5-x)].
经过分析之后,大家就可回答以上问题了.
[生](1)销售量可以表示为500+200(13.5-x)=3200-200x.
(2)销售额可以表示为x(3200-200x)=3200x-200x2.
(3)所获利润可以表示为(3200x-200x2)-2.5(3200-200x)=-200x2+3700x-8000.
(4)设总利润为y元,则
y=-200x2+3700x-8000
=-200(x-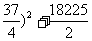 .
.
∵-200<0
∴抛物线有最高点,函数有最大值.
当x= =9.25元时,
=9.25元时,
y最大= 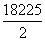 =9112.5元.
=9112.5元.
即当销售单价是9.25元时,可以获得最大利润,最大利润是9112.5元.
6. 何时获得最大利润
[基础练习]一、1. –1,小,5; 2. –3,大,. 二、1. (1)0≤x≤13,13<x≤30;(2)59;(3)13. 2. (1)月销售量450千克,月销售利润6 750元;(2)y = - 10x2 +1400x – 40 000;(3)80元.
[综合练习]750吨.
2. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克. 针对这种情况,解答以下问题:
(1)当销售单价定为每千克55元时,月销售量和月销售利润分别是多少?
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出x的取值范围);
(3)商店想在月销售成本不超过10 000元的情况下,使月销售利润达到8 000元,销售单价应定为每千克多少元?
[综合练习]
某公司某种产品的年产量不超过1 000吨,该产品的年产量(单位:吨)与费用(单位:万元)之间的函数图象是顶点在原点的抛物线的一部分(如图2-8);该产品的年销售量(单位:吨)与销售单价(单位:万元/吨)之间的函数图象是一条线段(如图2-9)若生产出的产品都能在当年销售完,问年产量为多少吨时,公司获得的毛利润最大(毛利润 = 销售额 – 费用)?

1. 心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(分)之间满足函数关系:y = -0.1x2 +2.6x + 43 (0≤x≤30).
(1)当x在什么范围内时,学生的接受能力逐步增强?当x在什么范围内时,学生的接受能力逐步减弱?
(2)第10分钟时,学生的接受能力是多少?
(3)第几分钟时,学生的接受能力最强?
2. 已知二次函数y = - ,当x = 时,y有最 值 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com