2．探索活动

　　 问题一　 在右图的直角三角形中，利用勾股定理可知 x=，根据已有的知识，你还知道哪些与这个三角形有关的数据信息吗?

　　 两个锐角都是45°，这个三角形的面积是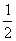，周长是2+，斜边上的高、中线是．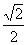

　　 问题二　 你知道与右图的三角形有关的哪些数据信息呢?

　　 问题三　 如果要知道一个等边三角形的有关信息，你认为至少需要哪些信息?与同学交流．

　　 问题一是把情境创设中的问题拓宽，为问题二、问题三作铺垫．通过对问题二、问题三的讨论交流，使学生主动地在等腰三角形、等边三角形中构造直角三角形，从而把解斜三角形的问题转化为解直角三角形的问题．

1．情境创设

　　 本课时的教学内容是勾股定理在数学内部的应用．课本设计用勾股定理探索一些无理数的活动，与本章第1节的“实验”，第2节的“由古巴比伦泥板上的一组数画三角形”相类似，都是为了使学生不断地感受“数”与“形”的内在联系、感受数学的整体性．

2．在运用勾股定理解决实际问题的过程中，感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题)，进一步发展有条理思考和有条理表达的能力，体会数学的应用价值．

[教学过程(第二课时)]

1．能运用勾股定理及直角三角形的判定条件解决实际问题．

2．7勾股定理的应用

[教学目标]

4．小结

举出生活中的近似数，指出它们精确到哪一位?各有几个有效数字?

3．例题教学

　　 (1)按四舍五人取近似数时，应提醒学生不能随便地将小数点后面的0去掉，比如，课本例1第(2)题；

　　 (2)例2教学时，建议让学生先讨论问题：

　　 某网站在某一时段网上访问人数约200200人，分别取这个数精确到万位的近似数和精确到千位的近似数．

　　 通过讨论使学生理解用科学记数法记数，不仅便于记一些较大(小)的数，而且易于表示近似数的有效数字．　　

2．关于近似数的精确度

　　 (1)近似数的精确度有两种意义：

　　 ①一个近似数四舍五人到哪一位，那么这个近似数精确到哪一位；

　　 ②由近似数的精确度可推断实际数所在的范围。例如，我国的国土面积约为959.7万km²，精确到0.1万km²，可以推断959.7万km²与我国国土的实际面积相差不大于0.05万km²，所以我国国土的实际面积在959.65km²到959.75km²之间；

　 　(2)近似数的精确度有两种形式：一是精确到哪一位；二是保留几个有效数字；

　　 (3)精确度的两种形式从不同的角度反映近似数的精确程度．例如，我国国土面积约为959.7万km²，俄罗斯的国土面积约为1707.0万km²，都是精确到 0.1万km²，与实际面积的误差都不大于0.05万km²．而从有效数字的角度可以看它们的精确程度不一样．这是因为，虽然它们与实际面积的误差都不大于 0.05万km²，但可以发现，测量中国国土面积平均每1万km²产生的误差是，约0.0052%；测量俄罗斯国土面积平均每1万km²产生的误差是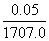，约 0.0030%．可见，几个近似数如果精确到的位数相同，那么有效数字越多的近似数，每单位量产生的误差就越小，因此它的精确程度相对也就越高．

1．情境创设

　　 除课本提供的情境外，还可以创设学生感兴趣、来源于现实世界和社会环境中的问题情境．例如，

　　 (1)从早晨起床到上学，你从你的生活环境中获得那些数的信息?

　　 (2)每天你看报吗?你平时从报纸上获取过哪些数的信息?

　　 (3)看电视时你最关心哪些有关数的信息?

　　 (4)生活中，有些数据是准确的，有些是近似的，你能举例说明吗?

　　 设计让学生自己搜集生活中与数有关的信息，从中进一步感受数的意义；认识生活中存在近似数和近似数在生活中的作用；了解测量长度、时间、速度等的结果是近似的；知道有时由于受客观条件的限制难以得到准确数，有时实际不需要准确数，计算中常常需要取一些数的近似数．

2．能说出一个近似数的精确度或有几个有效数字；能按照要求用四舍五入的方法，取一个数的近似数．

[教学过程]