
[师)我们已经做了不少用二次函数知识解决实际问题的例子,现在大家能否根据前面的例子作一下总结,解决此类问题的基本思路是什么呢?与同伴进行交流.
[生]首先是理解题目,然后是分析已知量与未知量,转化为数学问题.
[师]看来大家确实学会了用数学知识解决实际问题,基本思想如下:
投影片:(§2.7C)
解决此类问题的基本思路是:
(1)理解问题;
(2)分析问题中的变量和常量以及它们之间的关系;
(3)用数学的方式表示它们之间的关系;
(4)做函数求解;
(5)检验结果的合理性,拓展等.
在总结思路之前,大家已经做得相当出色了,相信以后会更上一层楼的.
Ⅲ.课堂练习
投影片:(§2.7 D)
1.一养鸡专业户计划用116 m长的竹篱笆靠墙(如下图)围成一个长方形鸡舍,怎样设计才能使围成的长方形鸡舍的面积最大?最大为多少?

解:设AB长为x m,则BC长为(116-2x)m,长方形面积为Sm2,根据题意得
S=x(116-2x)=-2x2+116x=-2(x2-58x+292-292)=-2(x-29)2+1682.
当x=29时,S有最大值1682,这时116-2x=58.
即设计成长为58 m,宽为29 m的长方形时,能使围成的长方形鸡舍的面积最大,最大面积为1682 m2.
Ⅳ.课时小结
本节课我们进一步学习了用二次函数知识解决最大面积问题,增强了应用意识,获得了利用数学方法解决实际问题的经验,并进一步感受了数学模型思想和数学的应用价值.
Ⅴ.课后作业
习题2.8
Ⅵ.活动与探究
已知矩形的长大于宽的2倍,周长为12,从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形的一边所成的角的正切值等于 .设梯形的面积为S,梯形中较短的底边长为x,试写出梯形面积关于x的函数关系式,并指出自变量x的取值范围.
.设梯形的面积为S,梯形中较短的底边长为x,试写出梯形面积关于x的函数关系式,并指出自变量x的取值范围.
分析:因为射线与矩形一边所成的角的正切值等于 ,但没有说明射线与矩形的哪一边所成角的正切值,故本题应考虑两种情况,如下图:
,但没有说明射线与矩形的哪一边所成角的正切值,故本题应考虑两种情况,如下图:

板书设计
§2.7 最大面积是多少
投影片:(§2.7 B)
某建筑物的窗户如下图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗户通过的光线最多(结果精确到0.01 m)?此时,窗户的面积是多少?

[师]通过刚才的练习,这个问题自己来解决好吗?
[生]可以.
分析:x为半圆的半径,也是矩形的较长边,因此x与半圆面积和矩形面积都有关系.要求透过窗户的光线最多,也就是求矩形和半圆的面积之和最大,即2xy+ x2最大,而由于4y+4x+3x+πx=7x+4y+πx=15,所以y=
x2最大,而由于4y+4x+3x+πx=7x+4y+πx=15,所以y= .面积S=
.面积S= πx2+2xy=
πx2+2xy= πx2+2x·
πx2+2x· =
= πx2+
πx2+ =-3.5x2+7.5x,这时已经转化为数学问题即二次函数了,只要化为顶点式或代入顶点坐标公式中即可.
=-3.5x2+7.5x,这时已经转化为数学问题即二次函数了,只要化为顶点式或代入顶点坐标公式中即可.
解:∵7x+4y-πx=15,
∴y= .
.
设窗户的面积是S(m2),则
S= πx2+2xy
πx2+2xy
= πx2+2x·
πx2+2x·
= πx2+
πx2+
=-3.5x2+7.5x
=-3.5(x2-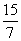 x)
x)
=-3.5(x- ).
).
∴当x= ≈1.07时,
≈1.07时,
S最大= ≈4.02.
≈4.02.
即当x≈1.07 m时,S最大≈4.02 m2,此时.窗户通过的光线最多.
[师]大家做得非常棒.
投影片;(§2.7 A)
如下图,在一个直角三角形的内部作一个长方形ABCD.其中AB和AD分别在两直角边上.

(1)设长方形的一边AB=x m,那么AD边的长度如何表示?
(2)设长方形的面积为y m2.当x取何值时,y的值最大?最大值是多少?
[师]分析:(1)要求AD边的长度,即求BC边的长度,而BC是△EBC中的一边,因此可以用三角形相似求出BC.由△EBC∽△EAF,得 所以AD=BC=
所以AD=BC= (40-x).
(40-x).
(2)要求面积夕的最大值.即求函数y=AB·AD=x· (40-x)的最大值,就转化为数学问题了.
(40-x)的最大值,就转化为数学问题了.
下面请大家讨论写出步骤.
[生](1)∵BC//AD,
∴△EBC∽△EAF. ∴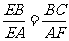 .
.
又AB=x,BE=40-x,
∴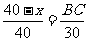 . ∴BC=
. ∴BC= (40-x).
(40-x).
∴AD=BC= (40-x)=30-
(40-x)=30- x.
x.
(2)y=AB·AD=x(30- x)= -
x)= - x2+30x
x2+30x
=- (x2-40x+400-400)
(x2-40x+400-400)
=- (x2-40x+400)+300
(x2-40x+400)+300
=- (x-20)2+300
(x-20)2+300
当x=20时, y最大=300.
即当x取20 m时,y的值最大,最大值是300m2.
[师]很好.刚才我们先进行了分析.要求面积就需要求矩形的两条边,把这两条边分别用含x的代数式表示出来,代入面积公式就能转化为数学问题了,大家觉得用数学知识解决实际问题很难吗?
[生]不很难.
[师]下面我们换一个条件.看看大家能否解决.设AD边的长为x m,则问题会怎样呢?与同伴交流.
[生]要求面积需求AB的边长,而AB=DC,所以需要求DC的长度,而DC是△FDC中的一边,所以可以利用三角形相似来求.
解:∵DC//AB,
∴△FDC∽△FAE.
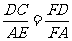 .
.
∵AD=x,FD=30-x.
∴ .
.
∴DC= (30-x).
(30-x).
∴AB=DC= (30-x).
(30-x).
y=AB·AD=x· (30-x)
(30-x)
=- x2+40x
x2+40x
=- (x2-30x+225-225)
(x2-30x+225-225)
=- (x-15)2+300.
(x-15)2+300.
当x=15时,y最大=300.
即当AD的长为15 m时,长方形的面积最大,最大面积是300 m2
备课资料(略)
3.议一议(投影片§2.7 C)
2.做一做(投影片§2.7 B)
[师)我们已经做了不少用二次函数知识解决实际问题的例子,现在大家能否根据前面的例子作一下总结,解决此类问题的基本思路是什么呢?与同伴进行交流.
[生]首先是理解题目,然后是分析已知量与未知量,转化为数学问题.
[师]看来大家确实学会了用数学知识解决实际问题,基本思想如下:
投影片:(§2.7C)
解决此类问题的基本思路是:
(1)理解问题;
(2)分析问题中的变量和常量以及它们之间的关系;
(3)用数学的方式表示它们之间的关系;
(4)做函数求解;
(5)检验结果的合理性,拓展等.
在总结思路之前,大家已经做得相当出色了,相信以后会更上一层楼的.
Ⅲ.课堂练习
投影片:(§2.7 D)
1.一养鸡专业户计划用116 m长的竹篱笆靠墙(如下图)围成一个长方形鸡舍,怎样设计才能使围成的长方形鸡舍的面积最大?最大为多少?

解:设AB长为x m,则BC长为(116-2x)m,长方形面积为Sm2,根据题意得
S=x(116-2x)=-2x2+116x=-2(x2-58x+292-292)=-2(x-29)2+1682.
当x=29时,S有最大值1682,这时116-2x=58.
即设计成长为58 m,宽为29 m的长方形时,能使围成的长方形鸡舍的面积最大,最大面积为1682 m2.
Ⅳ.课时小结
本节课我们进一步学习了用二次函数知识解决最大面积问题,增强了应用意识,获得了利用数学方法解决实际问题的经验,并进一步感受了数学模型思想和数学的应用价值.
Ⅴ.课后作业
习题2.8
Ⅵ.活动与探究
已知矩形的长大于宽的2倍,周长为12,从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形的一边所成的角的正切值等于 .设梯形的面积为S,梯形中较短的底边长为x,试写出梯形面积关于x的函数关系式,并指出自变量x的取值范围.
.设梯形的面积为S,梯形中较短的底边长为x,试写出梯形面积关于x的函数关系式,并指出自变量x的取值范围.
分析:因为射线与矩形一边所成的角的正切值等于 ,但没有说明射线与矩形的哪一边所成角的正切值,故本题应考虑两种情况,如下图:
,但没有说明射线与矩形的哪一边所成角的正切值,故本题应考虑两种情况,如下图:

板书设计
§2.7 最大面积是多少
投影片:(§2.7 B)
某建筑物的窗户如下图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗户通过的光线最多(结果精确到0.01 m)?此时,窗户的面积是多少?

[师]通过刚才的练习,这个问题自己来解决好吗?
[生]可以.
分析:x为半圆的半径,也是矩形的较长边,因此x与半圆面积和矩形面积都有关系.要求透过窗户的光线最多,也就是求矩形和半圆的面积之和最大,即2xy+ x2最大,而由于4y+4x+3x+πx=7x+4y+πx=15,所以y=
x2最大,而由于4y+4x+3x+πx=7x+4y+πx=15,所以y= .面积S=
.面积S= πx2+2xy=
πx2+2xy= πx2+2x·
πx2+2x· =
= πx2+
πx2+ =-3.5x2+7.5x,这时已经转化为数学问题即二次函数了,只要化为顶点式或代入顶点坐标公式中即可.
=-3.5x2+7.5x,这时已经转化为数学问题即二次函数了,只要化为顶点式或代入顶点坐标公式中即可.
解:∵7x+4y-πx=15,
∴y= .
.
设窗户的面积是S(m2),则
S= πx2+2xy
πx2+2xy
= πx2+2x·
πx2+2x·
= πx2+
πx2+
=-3.5x2+7.5x
=-3.5(x2-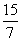 x)
x)
=-3.5(x- ).
).
∴当x= ≈1.07时,
≈1.07时,
S最大= ≈4.02.
≈4.02.
即当x≈1.07 m时,S最大≈4.02 m2,此时.窗户通过的光线最多.
[师]大家做得非常棒.
投影片;(§2.7 A)
如下图,在一个直角三角形的内部作一个长方形ABCD.其中AB和AD分别在两直角边上.

(1)设长方形的一边AB=x m,那么AD边的长度如何表示?
(2)设长方形的面积为y m2.当x取何值时,y的值最大?最大值是多少?
[师]分析:(1)要求AD边的长度,即求BC边的长度,而BC是△EBC中的一边,因此可以用三角形相似求出BC.由△EBC∽△EAF,得 所以AD=BC=
所以AD=BC= (40-x).
(40-x).
(2)要求面积夕的最大值.即求函数y=AB·AD=x· (40-x)的最大值,就转化为数学问题了.
(40-x)的最大值,就转化为数学问题了.
下面请大家讨论写出步骤.
[生](1)∵BC//AD,
∴△EBC∽△EAF. ∴ .
.
又AB=x,BE=40-x,
∴ . ∴BC=
. ∴BC= (40-x).
(40-x).
∴AD=BC= (40-x)=30-
(40-x)=30- x.
x.
(2)y=AB·AD=x(30- x)= -
x)= - x2+30x
x2+30x
=- (x2-40x+400-400)
(x2-40x+400-400)
=- (x2-40x+400)+300
(x2-40x+400)+300
=- (x-20)2+300
(x-20)2+300
当x=20时, y最大=300.
即当x取20 m时,y的值最大,最大值是300m2.
[师]很好.刚才我们先进行了分析.要求面积就需要求矩形的两条边,把这两条边分别用含x的代数式表示出来,代入面积公式就能转化为数学问题了,大家觉得用数学知识解决实际问题很难吗?
[生]不很难.
[师]下面我们换一个条件.看看大家能否解决.设AD边的长为x m,则问题会怎样呢?与同伴交流.
[生]要求面积需求AB的边长,而AB=DC,所以需要求DC的长度,而DC是△FDC中的一边,所以可以利用三角形相似来求.
解:∵DC//AB,
∴△FDC∽△FAE.
 .
.
∵AD=x,FD=30-x.
∴ .
.
∴DC= (30-x).
(30-x).
∴AB=DC= (30-x).
(30-x).
y=AB·AD=x· (30-x)
(30-x)
=- x2+40x
x2+40x
=- (x2-30x+225-225)
(x2-30x+225-225)
=- (x-15)2+300.
(x-15)2+300.
当x=15时,y最大=300.
即当AD的长为15 m时,长方形的面积最大,最大面积是300 m2
7.如图,有一座抛物线形拱桥,抛物线可用y=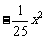 表示.在正常水位时水面AB
的宽为20m,如果水位上升3m时,水面CD的宽是10m.
表示.在正常水位时水面AB
的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)在正常水位时,有一艘宽8m、高2.5m的小船,它能通过这座桥吗?
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时, 忽然接到紧急通过:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行).试问:如果货车按原来的速度行驶,能否安全通过此桥?若能,请说明理由.若不能, 要使货车安全通过此桥,速度应超过每小时多少千米?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com