
1、经历探索二次函数与一元二次方程的关系的过程,体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性.
3、通过学生共同观察和讨论,培养合作交流意识.
2、通过观察二次函数与x 轴交点的个数,讨论一元二次方程的根的情况,进一步培养学生的数形结合思想.
1、经历探索二次函数与一元二次方程的关系的过程,培养学生的探索能力和创新精神
3、理解一元二次方程的根就是二次函数与y =h 交点的横坐标.
2、理解二次函数与x 轴交点的个数与一元二次方程的根的关系,理解何时方程有两个不等的实根、两个相等的实根和没有实根.
1、经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.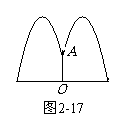 某公园要建造一个圆形喷水池,花形柱子OA竖立在水池中央,安装在柱子顶 端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过直线OA的任一平面上,抛物线形状如图2-17所示. 如图2-18建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之
某公园要建造一个圆形喷水池,花形柱子OA竖立在水池中央,安装在柱子顶 端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过直线OA的任一平面上,抛物线形状如图2-17所示. 如图2-18建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之
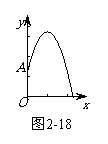
间的函数表达式是y = - x2 + 2x + . 请回答下列问题:
(1)柱子OA的高度是多少米?
(2)喷出的水流距水面的最大高度是多少米?
 (3)若不考虑其他因素,水池的半径至少需多少
(3)若不考虑其他因素,水池的半径至少需多少
米,才能使喷出的水流不至于落在池外?
[综合练习]
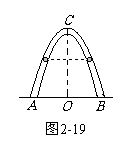 某校校门是一抛物线形建筑物(如图2-19),门高9米,两侧距地面5米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,求大门的地面宽度(建筑物的厚度忽略不计).
某校校门是一抛物线形建筑物(如图2-19),门高9米,两侧距地面5米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,求大门的地面宽度(建筑物的厚度忽略不计).
[探究练习]
已知二次函数y = kx2 + (2k –1)x
–1与x轴交点的横坐标为x1,x2 (x1 < x2),对于以下五个结论:①当x = -2时,y = 1;②当x >
x2时,y
> 0;③方程kx2 + (2k –1)x –1 = 0有两个不相等的实数根x1,x2;④x1
< -1,x2 > -1;⑤x2 - x1 = 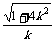 .请你说出哪些结论是正确的,为什么?
.请你说出哪些结论是正确的,为什么?
练习二
[基础练习]一、1. 2个,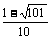 和
和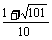 ; 2. x1
= -1、x2 = 3,-3. 二、1. 图略.(1)x1 =
-1.5,x2 = 2;(2)-1或1.5;(3)-1.5 < x
< 2. 2. (1)1.25米;(2)2.25米;(3)2.5米.
; 2. x1
= -1、x2 = 3,-3. 二、1. 图略.(1)x1 =
-1.5,x2 = 2;(2)-1或1.5;(3)-1.5 < x
< 2. 2. (1)1.25米;(2)2.25米;(3)2.5米.
[综合练习]9米(提示:以O为原点,AB为x轴建立直角坐标系,使抛物线的表达式为y = ax2 + 9的形式).
[探究练习]①、③、④是正确的.
1. 画出二次函数y = 2x2 – x – 6的图象,根据图象回答:
(1)方程2x2 – x – 6 = 0的根是什么?
(2)当x取什么值时,y的值等于-3?
(3)当x取什么值时,y的值小于0?
2. 二次函数y = x2 + bx + c的图象如图2-16所示,则关于x的一
元二次方程x2 + bx + c = 0的根是 ,当x = 2时,
y= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com