
2、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是
1、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标.
(1)y=6x2-2x+1 (2)y=-15x2+14x+8 (3)y=x2-4x+4
2、新课讲解
例题讲解
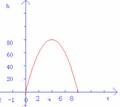 我们已经知道,竖直上抛物体的高度h (m )与运动时间t (s )的关系可以用公式
h =-5t 2+v 0t +h 0表示,其中h 0(m)是抛出时的高度,v 0(m/s
)是抛出时的速度.一个小球从地面被以40m/s 速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如下图所示,那么
我们已经知道,竖直上抛物体的高度h (m )与运动时间t (s )的关系可以用公式
h =-5t 2+v 0t +h 0表示,其中h 0(m)是抛出时的高度,v 0(m/s
)是抛出时的速度.一个小球从地面被以40m/s 速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如下图所示,那么
(1)h 与t 的关系式是什么?
(2)小球经过多少秒后落地?你有几种求解方法?
小组交流,然后发表自己的看法.
学生交流:(1)h 与t 的关系式是h =-5t 2+v 0t +h 0,其中的v 0
为40m/s,小球从地面抛起,所以h 0=0.把v 0,h 0带入上式即可
求出h 与t 的关系式h =-5t 2+40t
(2)小球落地时h为0 ,所以只要令h =-5t 2+v 0t +h 0中的h=0求出t即可.也就是
-5t 2+40t=0
t 2-8t=0
∴t(t-8)=0
∴t=0或t=8
t=0时是小球没抛时的时间,t=8是小球落地时的时间.
也可以观察图像,从图像上可看到t=8时小球落地.
议一议
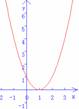
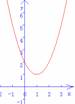
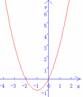
二次函数①y=x2+2x ②y=x2-2x+1③y=x2-2x +2 的图像如下图所示
(1)每个图像与x 轴有几个交点?
(2)一元二次方程x2+2x=0 , x2-2x+1=0有几个根?解方程验证一下, 一元二次方程x2-2x +2=0有根吗?
(3)二次函数的图像y=ax2+bx+c 与x 轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
学生讨论后,解答如下:
(1)二次函数①y=x2+2x ②y=x2-2x+1③y=x2-2x +2 的图像与x 轴分别有两个交点、一个交点,没有交点.
(2)一元二次方程x2+2x=0有两个根0,-2 ;x2-2x+1=0有两个相等的实数根1或一个根1 ;方程x2-2x +2=0没有实数根
(3)从图像和讨论知,二次函数y=x2+2x与x 轴有两个交点(0,0),(-2,0) ,方程x2+2x=0有两个根0,-2;
二次函数y=x2-2x+1的图像与x 轴有一个交点(1,0),方程 x2-2x+1=0有两个相等的实数根1或一个根1
二次函数y=x2-2x +2 的图像与x 轴没有交点, 方程x2-2x +2=0没有实数根
由此可知,二次函数y=ax2+bx+c 的图像与x 轴交点的横坐标即为一元二次方程ax2+bx+c=0的根.
小结:
二次函数y=ax2+bx+c 的图像与x 轴交点有三种情况:有两个交点、一个交点、没有焦点.当二次函数y=ax2+bx+c 的图像与x 轴有交点时,交点的横坐标就是当y =0时自变量x 的值,即一元二次方程ax2+bx+c=0的根.
基础练习
1、设问题情境,引入新课
我们已学过一元一次方程kx+b=0 (k≠0)和一次函数y =kx+b (k≠0)的关系,你还记得吗?
它们之间的关系是:当一次函数中的函数值y =0时,一次函数y =kx+b就转化成了一元一次方程kx+b=0,且一次函数的图像与x 轴交点的横坐标即为一元一次方程kx+b=0的解.
现在我们学习了一元二次方程和二次函数,它们之间是否也存在一定的关系呢?本节课我们将探索有关问题.
2、理解二次函数与x 轴交点的个数与一元二次方程的根的个数之间的关系.
教学方法
讨论探索法
教学过程:
1、探索方程与函数之间的联系的过程.
3.理解一元二次方程的根就是二次函数与y =h 交点的横坐标.
教学难点
2.理解何时方程有两个不等的实根、两个相等的实根和没有实根.
1.体会方程与函数之间的联系.
2、具有初步的创新精神和实践能力.
教学重点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com