
1.用定义法证明一个四边形是平行四边形时,要什么条件?
例1:已知:E、F分别为平行四边形ABCD两边
AD、BC的中点,连结BE、DF
求证: 图3
图3
分析:今天我们证明角相等,除了平行线,全等三角形外,又多了一个新方法,可以证明平行四边形对角相等,即只要四边形EBFD是平行四边形.由已知平行四边形ABCD的性质可得DE//BF,又AD=BC,E、F为中点则有DE=BF,根据“一组对边平行且相等的四边形是平行四边形”的判定定理,可得四边形EBFD是平行四边形.
证明由学生完成.
提问:此题还有什么方法,证明四边形BEDF是平行四边形.学生会想到证明 ,得到BE=DF,利用两组对边相等证明四边形是平行四边形.但应指出第二种方法较第一种方法繁,也就是说要找出较简捷的证法,准确地使用判定定理,就要先分析图形的性质,及所具备的条件.
,得到BE=DF,利用两组对边相等证明四边形是平行四边形.但应指出第二种方法较第一种方法繁,也就是说要找出较简捷的证法,准确地使用判定定理,就要先分析图形的性质,及所具备的条件.
练习:课本练习
小结
今天我们主要研究了利用边的关系来判定平行四边形,注意满足两个条件.

注意:若一组对边平行,另一组对边相等,是不可以判定为平行四边形的,它是梯形.
作业布置:1.课本.练习册相关内容.
设问:若一个四边形有一组对边平行且相等,能否判定这个四边形也是平行四边形呢?
活动:课本探究内容,并用事准备好的纸条(纸条的长度相等),先将纸条放置不平行位置,让学生设想若二纸条的端点为四边形的顶点,则组成的四边形是不是平行四边形?若将纸条摆放为平行的位置,则同样用二纸条的端点为顶点组成的四边形是不是平行四边形?
 设问:我们能否用推理的方法证明这个命题是正确的呢?(让学生找出题设、结论,然后写出已知、求证及证明过程.)
设问:我们能否用推理的方法证明这个命题是正确的呢?(让学生找出题设、结论,然后写出已知、求证及证明过程.)
小结:平行四边形判定方法五:
前提:若一个四边形有一组对边平行且相等.
结论:这个四边形是一个平行四边形.
如图用几何语言表达为:
∵AB=CD 且AB∥CD
 ∴四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
 平行且相等可用符号“ ”,读作“平行且相等”.
平行且相等可用符号“ ”,读作“平行且相等”.
∵AB CD
 ∴四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
(1).我们已学过哪些方法来判定一个四边形的平行四边形?(提问回答)
方法一(定义法):两组对边分别平行的四边形的平边形。
 几何语言表达定义法:
几何语言表达定义法:
∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形
解析:一个四边形只要其两组对边分别互相平行,
则可判定这个四边形是一个平行四边形。
活动:用做好的纸条拼成一个四边形,其中强调两组对边分别相等。
 方法二:两组对边分别相等的四边形是平行四边形。
方法二:两组对边分别相等的四边形是平行四边形。
设问:这个命题的前提和结论是什么?
已知:四边形ABCD中,AB=CD,AD=BC
求证:四边ABCD是平行四边形。
分析:判定平行四边形的依据目前只有定义,也就是须证明两组对边分别平行,当然是借助第三条直线证明角等。连结BD。易证三角形全等。(见图1)
板书证明过程。
 小结:用几何语言表达用定义法和刚才证明为正确的方法证明一个四边形是平行四边形的方法为:
小结:用几何语言表达用定义法和刚才证明为正确的方法证明一个四边形是平行四边形的方法为:
判定一:二组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,∴四边形ABCD是平行四边形
练习:课本P103练习题第1题。
例题讲解:
 例1 已知:如图3,E、F分别为平行四边形ABCD两边AD、BC的中点,连结BE、DF。
例1 已知:如图3,E、F分别为平行四边形ABCD两边AD、BC的中点,连结BE、DF。
求证:
分析:由我们学过平行四边形的性质中,对角
相等,得若证明四边形EBFD为平行四边形,便可得到 ,哪么如何证明该四边形为平行边形呢?可通过证明ΔABE≌ΔCDF得BE=DF;由AD=BC,E、F分别为AD和BC的中点得ED=FB。
,哪么如何证明该四边形为平行边形呢?可通过证明ΔABE≌ΔCDF得BE=DF;由AD=BC,E、F分别为AD和BC的中点得ED=FB。
 练习:2. 已知如图7,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH。
练习:2. 已知如图7,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH。
求证:四边形EFGH是平行四边形。
(让学生板演)
图7
本课小结:一个四边形二组对边分别平行或者相等的四边形是平行四边形这个判定定理来判定一个四边形是平行四边形。
作业布置:课本P100第4题、第7题。
8. 如图,李村有一口呈四边形的池塘,在它的四个角
如图,李村有一口呈四边形的池塘,在它的四个角 、
、 、
、 、
、 处均有一棵桃树,现在村委会准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持桃树不动,并要求扩建后的池塘呈平行四边形形状,请问该村能否实现这一设想?若能,请设计并画出图形,简单描述你的画法;若不能,请说明理由.
处均有一棵桃树,现在村委会准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持桃树不动,并要求扩建后的池塘呈平行四边形形状,请问该村能否实现这一设想?若能,请设计并画出图形,简单描述你的画法;若不能,请说明理由.
7.如图,平行四边形 中,试用三种方法将平行四边形分成面积相等的四部分.(要求用文字简述你所设计的三种方法,并在所给的三个平行四边形中正确画图)
中,试用三种方法将平行四边形分成面积相等的四部分.(要求用文字简述你所设计的三种方法,并在所给的三个平行四边形中正确画图)
6. 已知:如图, 、
、 是□
是□ 的对角线
的对角线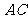 上的两点,且
上的两点,且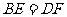 .
.
 求证:四边形
求证:四边形 是平行四边形.
是平行四边形.
5.在四边形 中,已知
中,已知 ∥
∥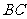 ,要使四边形
,要使四边形 为平行四边形,需要增加的条件是
(填一个你认为正确的条件).
为平行四边形,需要增加的条件是
(填一个你认为正确的条件).
4.□ 的周长是36㎝,
的周长是36㎝,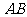 =8㎝,则
=8㎝,则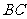 =
㎝.
=
㎝.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com