2．课本作业

设问：“对角线互相平分的四边形是平行四边形。”这一命题的前提什么？结论又是什么？

　　 活动：用事先准备好的纸条按课本探究方法做，让学生判定这个四边形是否是平行四边形。

判定方法三：对角线互相平分的四边形是平行四边形。

这个方法的前提是什么？结论又是什么？

已知：如图：在四边形ABCD中，AC、BD相交于O，OA=OC，OB=OD。

求证：四边形ABCD是平行四边形。

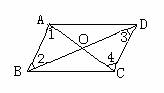分析：证明这个四边形是平行四边形的方法有：(1)两组对边分别相等；(2)平行四边形的定义：两组对边分别平行。(较简单的)

板书证过程。

小结：由刚才证明可得，只要有对角线互相

平分，可判定这个四边形是平行四边形。

几何语言表达：∵OA=OC， OB= OD　 ∴四边形ABCD是平行四边形

例题讲 解：课本P96例3。

分析：由题意可得OB=OD，再由OA=OF，AE=AF，可得OE=OF。可证四边形EBFD是平行四边形。

设问：若是两组对角分别相等的四边形，是不是平行四边形？前提是什么？结论是什么？　　　　　　　　　　　　　　　　

　　 A　　　　　　 B

已知：在四边形ABCD中，∠A =∠C

∠B=∠D。　　　　　　　　　　　　　　　　　　 D　　　　　　 C

　　 求证：四边形ABCD是平行四边形(让学生板书，然后小结)

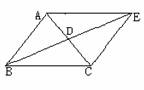练习：延长三角形ABC的中线BD至E，

使DE=BD，连结AE、CE，如图，

求证：∠BAE=∠BCE。

证明方法：由对角线互相平分可证四边形ABCE为平行四边形，可得∠BAE=∠BCE。

本课小结：　 目前，我们研究平行四边形的哪些性质和判定：

平行四边形的性质：对边平行；对边相等；对角线互相平分；夹在平行线间的平行线段相等；对角相等；邻角互补；

平行四边形的判定：两组对边平行；两组对边相等；两组对角相等；对角线互相平分的四边形；

作业布置：　　

1、熟记判定定理；　

3．平行四边形的对角线互相平分的逆命题如何表达？是否是真命题？

2．用所学的判定方法一判定一个四边形的平行四边形的条件是什么？

1．用定义法证明一个四边形是平行四边形时，要什么条件？

方法一(定义法)：两组对边分别平行的四边形的平边形。

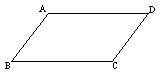几何语言表达定义法：

∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形

解析：一个四边形只要其两组对边分别互相平行，

则可判定这个四边形是一个平行四边形。

活动：用做好的纸条拼成一个四边形，其中强调两组对边分别相等。

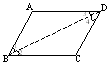方法二：两组对边分别相等的四边形是平行四边形。

设问：这个命题的前提和结论是什么？

　　 已知：四边形ABCD中，AB＝CD，AD＝BC

　　 求证：四边ABCD是平行四边形。

　　 分析：判定平行四边形的依据目前只有定义，也就是须证明两组对边分别平行，当然是借助第三条直线证明角等。连结BD。易证三角形全等。(见图1)

　　 板书证明过程。

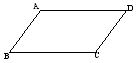小结：用几何语言表达用定义法和刚才证明为正确的方法证明一个四边形是平行四边形的方法为：

判定一：二组对边分别相等的四边形是平行四边形

∵AB=CD，AD=BC，∴四边形ABCD是平行四边形

练习：课本P103练习题第1题。

例题讲解：

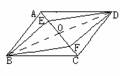
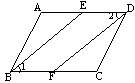例1 　已知：如图3，E、F分别为平行四边形ABCD两边AD、BC的中点，连结BE、DF。

　　 求证：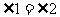

分析：由我们学过平行四边形的性质中，对角

相等，得若证明四边形EBFD为平行四边形，便可得到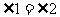，哪么如何证明该四边形为平行边形呢？可通过证明ΔABE≌ΔCDF得BE=DF；由AD=BC，E、F分别为AD和BC的中点得ED=FB。

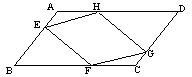练习：2. 已知如图7，E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点，且AE＝CG，BF＝DH。

　　 求证：四边形EFGH是平行四边形。

　(让学生板演)

　　　　　　　　　　　　　　　　　 图7

本课小结：一个四边形二组对边分别平行或者相等的四边形是平行四边形这个判定定理来判定一个四边形是平行四边形。

作业布置：课本P100第4题、第7题。

2．课本作业

设问：“对角线互相平分的四边形是平行四边形.”这一命题的前提什么？结论又是什么？

　　 活动：用事先准备好的纸条按课本探究方法做，让学生判定这个四边形是否是平行四边形.

判定方法三：对角线互相平分的四边形是平行四边形.

这个方法的前提是什么？结论又是什么？

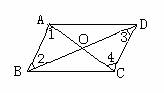
已知：如图：在四边形ABCD中，AC、BD相交于O，OA=OC，OB=OD.

求证：四边形ABCD是平行四边形.

分析：证明这个四边形是平行四边形的方法有：(1)两组对边分别相等；(2)平行四边形的定义：两组对边分别平行.(较简单的)

板书证过程.

小结：由刚才证明可得，只要有对角线互相

平分，可判定这个四边形是平行四边形.

几何语言表达：∵OA=OC， OB= OD　 ∴四边形ABCD是平行四边形

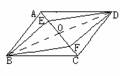
例题讲　 解：课本P96例3.

分析：由题意可得OB=OD，再由OA=OF，AE=AF，可得OE=OF.可证四边形EBFD是平行四边形.

设问：若是两组对角分别相等的四边形，是不是平行四边形？前提是什么？结论是什么？　　　　　　　　　　　　　　　　

　　 A　　　　　　 B

已知：在四边形ABCD中，∠A =∠C

∠B=∠D.　　　　　　　　　　　　　　　　　　 D　　　　　　 CC

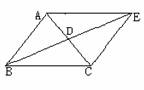　　 求证：四边形ABCD是平行四边形(让学生板书，然后小结)

练习：延长三角形ABC的中线BD至E，

使DE=BD，连结AE、CE，如图，

求证：∠BAE=∠BCE.

证明方法：由对角线互相平分可证四边形ABCE为平行四边形，可得∠BAE=∠BCE.

本课小结：　 目前，我们研究平行四边形的哪些性质和判定：

平行四边形的性质：对边平行；对边相等；对角线互相平分；夹在平行线间的平行线段相等；对角相等；邻角互补；

平行四边形的判定：两组对边平行；两组对边相等；两组对角相等；对角线互相平分的四边形；

作业布置：　　

1、熟记判定定理；　

3．平行四边形的对角线互相平分的逆命题如何表达？是否是真命题？

2．用所学的判定方法一判定一个四边形的平行四边形的条件是什么？