7. 学校体育节前一位同学在进行投掷训练中，投了20次标枪，其中3次投了45米，8次投了45.8米，7次投了45.4米，1次投了46.1米，1次犯规，求这位同学每次投掷标枪党的米数的众数、中位数和平均数。

6. 已知一组数据为0，1，5，x，7，且这组数据的中位数是5，那么x的取值为(　　 )

　 A. x＝5　　　　 B. x＜5　　　　 C. x≥5　　　　 D. x≠5

5. 下列说法真确的是(　　 )

　 A. 样本7，7，6，5，4的众数是2

　 B. 若数据x₁，x₂，…x_n的平均数是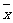，则(x_1­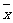－)+(x₂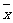－)+…+(x_n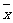－)＝0

　 C. 样本1，2，3，4，5，6的中位数是4

　 D. 样本50，50，39，41，41不存在众数

4. 已知一组数据：x₁＝4，x₂＝5，x₃＝6，x₄＝7，它们出现的次数依次为2，3，2，1，则这组数据的众数为　　　 ，中位数为　　　 ，平均数为　　　 。

3. 一次英语口语测试中，20名学生的得分如下：

　 70，80，100，60，80，70，90，50，80，70，80，70，90，80，90，80，70，90，60，80。

　 这次英语口试中学生得分的众数是　　 ，中位数是　　　 。

2. 一组数据中出现次数　　　　 的数据就是这组数据的众数，众数可以有　　　 个。

1. 已知一组数据的中位数为80，可知这组数据中大于或小于这个中位数的数据各占　　　 ，中位数有　　 个。

例1：已知：E、F分别为平行四边形ABCD两边

AD、BC的中点，连结BE、DF

　　 求证：　　　　　　　　　　　　　　　　 图3

分析：今天我们证明角相等，除了平行线，全等三角形外，又多了一个新方法，可以证明平行四边形对角相等，即只要四边形EBFD是平行四边形。由已知平行四边形ABCD的性质可得DE//BF，又AD＝BC，E、F为中点则有DE＝BF，根据“一组对边平行且相等的四边形是平行四边形”的判定定理，可得四边形EBFD是平行四边形。

　　 证明由学生完成。

　　 提问：此题还有什么方法，证明四边形BEDF是平行四边形。学生会想到证明，得到BE＝DF，利用两组对边相等证明四边形是平行四边形。但应指出第二种方法较第一种方法繁，也就是说要找出较简捷的证法，准确地使用判定定理，就要先分析图形的性质，及所具备的条件。

练习：课本练习

小结

　　 今天我们主要研究了利用边的关系来判定平行四边形，注意满足两个条件。

　　 注意：若一组对边平行，另一组对边相等，是不可以判定为平行四边形的，它是梯形。

作业布置：1．课本．练习册相关内容。

设问：若一个四边形有一组对边平行且相等，能否判定这个四边形也是平行四边形呢？

活动：课本探究内容，并用事准备好的纸条(纸条的长度相等)，先将纸条放置不平行位置，让学生设想若二纸条的端点为四边形的顶点，则组成的四边形是不是平行四边形？若将纸条摆放为平行的位置，则同样用二纸条的端点为顶点组成的四边形是不是平行四边形？

设问：我们能否用推理的方法证明这个命题是正确的呢？(让学生找出题设、结论，然后写出已知、求证及证明过程。)

小结：平行四边形判定方法五：

前提：若一个四边形有一组对边平行且相等。

结论：这个四边形是一个平行四边形。

如图用几何语言表达为：

∵AB=CD 且AB∥CD

∴四边形ABCD是平行四边形

平行且相等可用符号“　 ”，读作“平行且相等”。

∵AB　 CD

∴四边形ABCD是平行四边形

　　 (1)．我们已学过哪些方法来判定一个四边形的平行四边形？(提问回答)