
4、在一次英语口试中,已知50分1人、60分2人、70分5人、90分5人、100分1人,其余为84分。已知该班平均成绩为80分,问该班有多少人?
答案:1.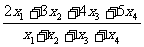 2.
2.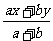 3.
3.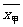 =86.9
=86.9 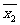 =96.5
=96.5
乙被录取 4. 39人
3、一家公司打算招聘一名部门经理,现对甲、乙两名应聘者从笔试、面试、实习成绩三个方面表现进行评分,笔试占总成绩20%、面试占30%、实习成绩占50%,各项成绩如表所示:
|
应聘者 |
笔试 |
面试 |
实习 |
|
甲 |
85 |
83 |
90 |
|
乙 |
80 |
85 |
92 |
试判断谁会被公司录取,为什么?
2、某人打靶,有a次打中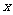 环,b次打中
环,b次打中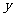 环,则这个人平均每次中靶 环。
环,则这个人平均每次中靶 环。
1、在一个样本中,2出现了x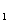 次,3出现了x
次,3出现了x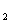 次,4出现了x
次,4出现了x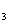 次,5出现了x
次,5出现了x 次,则这个样本的平均数为 .
次,则这个样本的平均数为 .
2、为了鉴定某种灯泡的质量,对其中100只灯泡的使用寿命进行测量,结果如下表:(单位:小时)
|
寿命 |
450 |
550 |
600 |
650 |
700 |
|
只数 |
20 |
10 |
30 |
15 |
25 |
求这些灯泡的平均使用寿命?
答案:1.
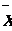
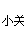 =79.05
=79.05 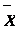
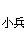 =80 2.
=80 2. 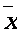 =597.5小时
=597.5小时
1、老师在计算学期总平均分的时候按如下标准:作业占100%、测验占30%、期中占35%、期末考试占35%,小关和小兵的成绩如下表:
|
学生 |
作业 |
测验 |
期中考试 |
期末考试 |
|
小关 |
80 |
75 |
71 |
88 |
|
小兵 |
76 |
80 |
68 |
90 |
例1和例2均为计算数据加权平均数型问题,因为是初学尤其之前与平均数计算公式已经作过比较,所以这里应该让学生搞明白问题中是否有权数,即是选择普通的平均数计算还是加权平均数计算,其次若用加权平均数计算,权数又分别是多少?例2的题意理解很重要,一定要让学生体会好这里的几个百分数在总成绩中的作用,它们的作用与权的意义相符,实际上这几个百分数分别表示几项成绩的权。
1、若不选择教材中的引入问题,也可以替换成更贴近学生学习生活中的实例,下举一例可供借鉴参考。
某校初二年级共有4个班,在一次数学考试中参考人数和成绩如下:
|
班级 |
1班 |
2班 |
3班 |
4班 |
|
参考人数 |
40 |
42 |
45 |
32 |
|
平均成绩 |
80 |
81 |
82 |
79 |
求该校初二年级在这次数学考试中的平均成绩?下述计算方法是否合理?为什么?
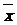 =
=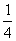 (79+80+81+82)=80.5
(79+80+81+82)=80.5
3、教材P138例2的作用如下:
(1)、这个例题再次将加权平均数的计算公式得以及时巩固,让学生熟悉公式的使用和书写步骤。
(2)、例2与例1的区别主要在于权的形式又有变化,以百分数的形式出现,升华了学生对权的意义的理解。
(3)、它也充分体现了统计知识在实际生活中的广泛应用。
2、教材P137例1的作用如下:
(1)、解决例1要用到加权平均数公式,所以说它最直接、最重要的目的是及时复习巩固公式,并且举例说明了公式用法和解题书写格式,给学生以示范和模仿。
(2)、这里的权没有直接给出数量,而是以比的形式出现,为加深学生对权的意义的理解。
(3)、两个问题中的权数各不相同,直接导致结果有所不同,这既体现了权数在求加权平均数的作用,又反映了应用统计知识解决实际问题时要灵活、体现知识要活学活用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com