
3.思考题:已知如图3, 是矩形
是矩形 对角线交点,
对角线交点, 平分
平分 ,
, ,求
,求 的度数(让学生板书,然后教师讲评)
的度数(让学生板书,然后教师讲评)
制一个活动的平行四边形教具,堂上进行演示图,使学生注意观察四边形角的变化,当变到一个角是直角时,指出这时平行四边形是矩形,使学生明确矩形是特殊的平行四边形(特殊之处就在于一个角是直角,深刻理解矩形与平行四边形的联系和区别).
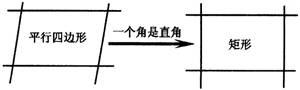
矩形的性质:既然矩形是一种特殊的平行四边形,就应具有平行四边形性质,同时矩形又是特殊的平行四边形,比平行四边形多了一个角是直角的条件,因而它就增加了一些特殊性质.
矩形性质1:矩形的四个角都是直角.
矩形性质2:矩形对角线相等.
设问:如何用理论推理的方法来证明矩形的对角线相等呢?(让学生思考并提问回答,再让学生板书)
讲矩形判定定理1,对角线相等的平行四边形是矩形。
已知:在平行四边形ABCD中,AC=DB, 求证:平行四边形ABCD是矩形。
证明:∵四边形ABCD是平行四边形,

 ∴AB=DC。务员
A
D
∴AB=DC。务员
A
D
又∵AC=DB,BC=CB,
∴△ABC≌△DCB。
∴∠ABC=∠DCB。 B C
又∵AB∥DC,
∴∠ABC+∠DCB=180°。
∴∠ABC=90°。
∴四边形ABCD是矩形。例题讲解:(强调这种计算题的解题格式,防止学生离开几何元素之间的关系,而单纯进行代数计算)
矩形判定定理1。除用定义判定矩形外,还有什么方法判定一个四边形或平行四边形是矩形呢?(引导学生从平行四边形性质定理与判定定理的关系考虑)
定理2 有三个角是直角的四边形是矩形。
问:矩形判定定理1是矩形性质定理1的逆定理吗?(不是)
判定定理的对象是四边形还是平行四边形?(四边形)
 谁能口述证明?
A
B
谁能口述证明?
A
B
证明:∵∠A+∠B+∠C+∠D=360°,
∠A=∠B=∠C=90°,
∴∠D=90°
∴AB∥CD,AD∥BC D C
又∵∠A=90°,
∴四边形ABCD是矩形。(有一个角是直角的平行四边形是矩形)
矩形的判定方法有哪些?
 一个角是直角的平行四边形
一个角是直角的平行四边形
对角线相等的平行四边形 --是矩形。
有三个角是直角的四边形
(2)要注意不要不加考虑地把性质定理的逆命题作为矩形的判定定理.
补充例题
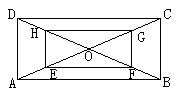 例1:已知:O是矩形ABCD对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,AE=BF=CG=DH,
例1:已知:O是矩形ABCD对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,AE=BF=CG=DH,
求证:四边形EFGH为矩形
分析:利用对角线互相平分且相等的四边形是矩形可以证明
证明:∵ABCD为矩形
∴AC=BD
∴AC、BD互相平分于O
∴AO=BO=CO=DO
∵AE=BF=CG=DH
∴EO=FO=GO=HO
又HF=EG
∴EFGH为矩形
例2:判断
(1)两条对角线相等四边形是矩形( )
(2)两条对角线相等且互相平分的四边形是矩形( )
(3)有一个角是直角的四边形是矩形( )
(4)在矩形内部没有和四个顶点距离相等的点( )
分析及解答:
(1)如图(1)四边形ABCD中,AC=BD,但ABCD不为矩形,∴×
(2)对角线互相平分的四边形即平行四边形,∴对角线相等的平行四边形为矩形∴√
(3)如图(2),四边形ABCD中,∠B=90°,但ABCD不为矩形 ∴×
(4)矩形对角线的交点O到四个顶点距离相等 ∴×, 如图(3),

3. 矩形知识的综合应用。(让学生思考,然后师生共同完成)
矩形知识的综合应用。(让学生思考,然后师生共同完成)
例:已知
 的对角线
的对角线 ,
, 相交于
相交于
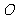 ,△
,△ 是等边三角形,
是等边三角形,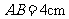 ,求这个平行
,求这个平行
四边形的面积(图2).
分析解题思路:(1)先判定
 为矩形.(2)求出
为矩形.(2)求出 △
△ 的直角边
的直角边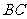 的长.(3)计算
的长.(3)计算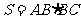 .
.
2.矩形判定方法的实际应用
除教材中所举的门框或矩形零件外,还可以结合生产生活实际说明判定矩形的实用价值.
设问:1.矩形的判定.
2.矩形是有一个角是直角的平行四边形,在判定一个四边形是不是矩形,首先看这个四边形是不是平行四边形,再看它两边的夹角是不是直角,这种用“定义”判定是最重要和最基本的判定方法(这体现了定义作用的双重性、性质和判定).除此之外,还有其它几种判定矩形的方法,下面就来研究这些方法.
方法1:有三个角是直角的四边形是矩形.(并让学生写出推理过程。)
矩形判定方法2:对角钱相等的平行四边形是矩形.(分析判定方法2和学生一道写出证明过程。)
归纳矩形判定方法(由学生小结):
(1)一个角是直角的平行四边形.(2)对角线相等的平行四边形.
(3)有三个角是直角的四边形.
3.矩形与平行四边形有什么共同之处?有什么不同之处?
2.矩形有哪些性质?
图3
3. 思考题:已知如图3,
思考题:已知如图3, 是矩形
是矩形 对角线交点,
对角线交点,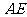 平分
平分 ,
, ,求
,求 的度数(让学生板书,然后教师讲评)
的度数(让学生板书,然后教师讲评)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com