
3. 难点的突破方法:
方差公式:S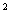 =
=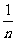 [(
[(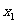 -
-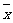 )
)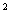 +(
+(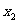 -
-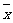 )
)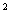 +…+(
+…+( -
-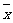 )
)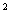 ]比较复杂,学生理解和记忆这个公式都会有一定困难,以致应用时常常出现计算的错误,为突破这一难点,我安排了几个环节,将难点化解。
]比较复杂,学生理解和记忆这个公式都会有一定困难,以致应用时常常出现计算的错误,为突破这一难点,我安排了几个环节,将难点化解。
(1)首先应使学生知道为什么要学习方差和方差公式,目的不明确学生很难对本节课内容产生兴趣和求知欲望。教师在授课过程中可以多举几个生活中的小例子,不如选择仪仗队队员、选择运动员、选择质量稳定的电器等。学生从中可以体会到生活中为了更好的做出选择判断经常要去了解一组数据的波动程度,仅仅知道平均数是不够的。
(2)波动性可以通过什么方式表现出来?第一环节中点明了为什么去了解数据的波动性,第二环节则主要使学生知道描述数据,波动性的方法。可以画折线图方法来反映这种波动大小,可是当波动大小区别不大时,仅用画折线图方法去描述恐怕不会准确,这自然希望可以出现一种数量来描述数据波动大小,这就引出方差产生的必要性。
(3)第三环节 教师可以直接对方差公式作分析和解释,波动大小指的是与平均数之间差异,那么用每个数据与平均值的差完全平方后便可以反映出每个数据的波动大小,整体的波动大小可以通过对每个数据的波动大小求平均值得到。所以方差公式是能够反映一组数据的波动大小的一个统计量,教师也可以根据学生程度和课堂时间决定是否介绍平均差等可以反映数据波动大小的其他统计量。
2. 难点:理解方差公式
1. 重点:方差产生的必要性和应用方差公式解决实际问题。
3. 会用方差计算公式来比较两组数据的波动大小。
2. 理解方差概念的产生和形成的过程。
1. 了解方差的定义和计算公式。
20.2.1极差
|
教学目标 |
知识与技能 |
1.理解极差的概念,知道极差等于一组数据中最大数与最小数的差. 2.引导学生发现极差能反映一组数据中两个极端值之间的差异情况,是刻画一组数据离散程度的一个统计量. 3.能够列举几个利用极差进行比较的实例. 4.生体会数学与生活密切相关 |
|
过程与方法 |
通过一系列富有启发性、层层深入的问题,引导学生广泛思考和探索.通过对解决问题的反思获得解决问题的经验,结实显示生活中的现象. |
|
|
情感态度与价值观 |
通过与生活实际紧密联系的大量问题的解决,引发学生学习数学的兴趣,体会数学源于生活;通过与数据集中趋势比较学习,培养学生独立思考、勇于创新的科学精神,并形成实事求是的科学态度. |
|
|
重点 |
极差概念的理解 |
|
|
难点 |
极差概念的引入 |
教 学 过 程
|
备 注 |
教学设计 与 师生互动 |
||||||||||||||||||||||
|
|
第一步:创设情景: 问题:为了比较甲、乙两种棉花品种的好坏,任意抽取每种棉花各10棵,统计它们结桃数的情况如下:
你认为两种棉花哪种结桃情况较好? 操作:让学生在各个的学习小组中讨论、解释、交流自己的发现.教师可以参与到某个或几个小组中倾听.在小组学习中讨论、交流发现另一个统计量极差(它有别于平均数、众数、中位数),极差反映了一组数据的离散程度. 思考:你能获取什么信息呢? 发现1.甲种棉花结桃的最多数目为89,最少数目为79,其差为10;乙种棉花结桃的最多数目为91,最少数目为76,其差为15. 发现2.乙种棉花的结桃数据较甲种棉花的结桃更分散,分散的程度较大,说明棉花的结桃情况越不稳定. 通过以上发现可知:甲种棉花的结桃情况较乙种棉花好 |
||||||||||||||||||||||
|
第二步:归纳总结: 极差定义:一组数据的最大数据与最小数据的差叫这组数据的极差. 表达式:极差=最大值-最小值 总结: 1. 极差是刻画数据离散程度的最简单的统计量 2. 特点是计算简单 3. 极差是利用了一组数据两端的信息,但不能反映出中间数据的分散状况 注意:极差反映一组数据两个极端值之间的差异情况,仅由两个数据评判一组数据是不科学的,要了解其他的统计量,在此为下一节的内容埋下伏笔. |
|||||||||||||||||||||||
|
第三步;随堂练习: 1、一组数据:473、865、368、774、539、474的极差是 ,一组数据1736、1350、-2114、-1736的极差是 . 2、一组数据3、-1、0、2、X的极差是5,且X为自然数,则X= . 3、下列几个常见统计量中能够反映一组数据波动范围的是( ) A.平均数 B.中位数 C.众数 D.极差 4、一组数据X 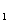 、X 、X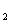 …X …X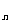 的极差是8,则另一组数据2X 的极差是8,则另一组数据2X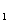 +1、2X +1、2X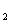 +1…,2X +1…,2X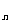 +1的极差是( ) +1的极差是( )A. 8 B.16 C.9 D.17 答案:1. 497、3850 2. 4 3. D 4.B |
|||||||||||||||||||||||
|
第四步;课后练习: 1、已知样本9.9、10.3、10.3、9.9、10.1,则样本极差是( ) A. 0.4 B.16 C.0.2 D.无法确定 在一次数学考试中,第一小组14名学生的成绩与全组平均分的差是2、3、-5、10、12、8、2、-1、4、-10、-2、5、5、-5,那么这个小组的平均成绩是( ) A. 87 B. 83 C. 85 D无法确定 3、已知一组数据2.1、1.9、1.8、X、2.2的平均数为2,则极差是 . 4、若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 . 5、某活动小组为使全小组成员的成绩都要达到优秀,打算实施“以优帮困”计划,为此统计了上次测试各成员的成绩(单位:分) 90、95、87、92、63、54、82、76、55、100、45、80 计算这组数据的极差,这个极差说明什么问题? 将数据适当分组,做出频率分布表和频数分布直方图. 答案:1.A ; 2.D ; 3. 0.4 ; 4.30、40. 5(1)极差55分,从极差可以看出这个小组成员成绩优劣差距较大.(2)略 |
|||||||||||||||||||||||
|
第五步:课堂小结 本节课我们主要学习了 1、 极差--反映一组数据变化范围的大小 2、极差=最大值-最小值 3、极差在分析一组数据的离散程度时,仍有不足的一面. |
|||||||||||||||||||||||
|
课后反思:本节课创设恰当的问题情景,激发了学生的兴趣与思考.引导学生把数据转化成图象,观察、比较、分析从另一个角度来刻画这组数据的变化范围.巧妙地引出极差概念,体会概念的形成过程,接着呈现多种形式的问题,通过思考、合作交流进一步理解极差概念.使学生学会收集、整理、分析数据,逐步地掌握统计思想. |
90、95、87、92、63、54、82、76、55、100、45、80
计算这组数据的极差,这个极差说明什么问题?
将数据适当分组,做出频率分布表和频数分布直方图。
答案:1.A ; 2.D ; 3. 0.4 ; 4.30、40. 5(1)极差55分,从极差可以看出这个小组成员成绩优劣差距较大。(2)略
5、某活动小组为使全小组成员的成绩都要达到优秀,打算实施“以优帮困”计划,为此统计了上次测试各成员的成绩(单位:分)
4、若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com