
20.3 菱形的判定 同步练习
目标与方法
20.2.2 方差
|
教学目标 |
知识与技能 |
1. 了解方差的定义和计算公式. 2. 理解方差概念的产生和形成的过程. 3. 会用方差计算公式来比较两组数据的波动大小. |
|
过程与方法 |
经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验. |
|
|
情感态度与价值观 |
培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义. |
|
|
重点 |
方差产生的必要性和应用方差公式解决实际问题.掌握其求法. |
|
|
难点 |
理解方差公式,应用方差对数据波动情况的比较、判断. |
教学过程
|
备 注 |
教学设计 与 师生互动 |
|||||||||||||||||||||||||||||||||||
|
|
第一步:情景创设 乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测.结果如下(单位:mm): A厂:40.0,39.9,40.0,40.1,40.2,39.8,40.0,39.9,40.0,40.1; B厂:39.8,40.2,39.8,40.2,39.9,40.1,39.8,40.2,39.8,40.2. 你认为哪厂生产的乒乓球的直径与标准的误差更小呢? (1) 请你算一算它们的平均数和极差. (2) 是否由此就断定两厂生产的乒乓球直径同样标准? 今天我们一起来探索这个问题. 探索活动 通过计算发现极差只能反映一组数据中两个极值之间的大小情况,而对其他数据的波动情况不敏感.让我们一起来做下列的数学活动 算一算 把所有差相加,把所有差取绝对值相加,把这些差的平方相加. 想一想 你认为哪种方法更能明显反映数据的波动情况? |
|||||||||||||||||||||||||||||||||||
|
第二步:讲授新知: (一)方差 定义:设有n个数据 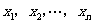 ,各数据与它们的平均数的差的平方分别是 ,各数据与它们的平均数的差的平方分别是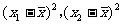 ,…, ,…,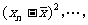 我们用它们的平均数,即用 我们用它们的平均数,即用 来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作  . .意义:用来衡量一批数据的波动大小 在样本容量相同的情况下,方差越大,说明数据的波动越大, 越不稳定 归纳:(1)研究离散程度可用 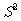 (2)方差应用更广泛衡量一组数据的波动大小 (3)方差主要应用在平均数相等或接近时 (4)方差大波动大,方差小波动小,一般选波动小的 方差的简便公式: 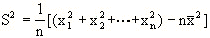 推导:以3个数为例 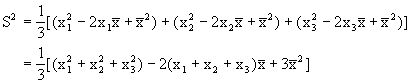  (二)标准差: 方差的算术平方根,即 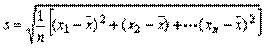 ④ ④并把它叫做这组数据的标准差.它也是一个用来衡量一组数据的波动大小的重要的量. 注意:波动大小指的是与平均数之间差异,那么用每个数据与平均值的差完全平方后便可以反映出每个数据的波动大小,整体的波动大小可以通过对每个数据的波动大小求平均值得到.所以方差公式是能够反映一组数据的波动大小的一个统计量,教师也可以根据学生程度和课堂时间决定是否介绍平均差等可以反映数据波动大小的其他统计量. |
||||||||||||||||||||||||||||||||||||
|
第三步:解例分析: 例1 填空题; (1)一组数据: 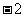 , ,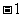 ,0, ,0,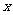 ,1的平均数是0,则 ,1的平均数是0,则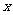 = .方差 = .方差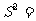 .
.(2)如果样本方差 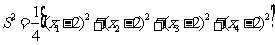 , ,那么这个样本的平均数为 .样本容量为 . (3)已知 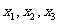 的平均数 的平均数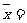 10,方差 10,方差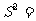 3,则 3,则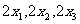 的平均数为
,方差为
. 的平均数为
,方差为
.例2 选择题: (1)样本方差的作用是( ) A、估计总体的平均水平 B、表示样本的平均水平 C、表示总体的波动大小 D、表示样本的波动大小,从而估计总体的波动大小 (2)一个样本的方差是0,若中位数是 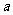 ,那么它的平均数是( ) ,那么它的平均数是( )A、等于 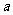 B、不等于
B、不等于 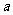 C、大于 C、大于 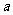 D、小于 D、小于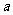 (3)已知样本数据101,98,102,100,99,则这个样本的标准差是( ) A、0 B、1 C、 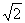 D、2
D、2(4)如果给定数组中每一个数都减去同一非零常数,则数据的( ) A、平均数改变,方差不变 B、平均数改变,方差改变 C、平均数不变,方差不变 A、平均数不变,方差改变 例3 为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下:(单位:mm) 甲:9,10,11,12,7,13,10,8,12,8 乙:8,13,12,11,10,12,7,7,9,11 请你经过计算后回答如下问题: (1)哪种农作物的10株苗长的比较高? (2)哪种农作物的10株苗长的比较整齐? P154例1 分析应注意的问题:题目中“整齐”的含义是什么?说明在这个问题中要研究一组数据的什么?学生通过思考可以回答出整齐即波动小,所以要研究两组数据波动大小,这一环节是明确题意. 1. 在求方差之前先要求哪个统计量,为什么?学生也可以得出先求平均数,因为公式中需要平均值,这个问题可以使学生明确利用方差计算步骤. 2. 方差怎样去体现波动大小? 这一问题的提出主要复习巩固方差,反映数据波动大小的规律. |
||||||||||||||||||||||||||||||||||||
|
第四步:随堂练习: 1. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm) 甲:9、10、11、12、7、13、10、8、12、8; 乙:8、13、12、11、10、12、7、7、9、11; 问:(1)哪种农作物的苗长的比较高? (2)哪种农作物的苗长得比较整齐? 2. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
2. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
1. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm) 甲:9、10、11、12、7、13、10、8、12、8; 乙:8、13、12、11、10、12、7、7、9、11; 问:(1)哪种农作物的苗长的比较高? (2)哪种农作物的苗长得比较整齐? 3. 方差怎样去体现波动大小? 这一问题的提出主要复习巩固方差,反映数据波动大小的规律。 2. 在求方差之前先要求哪个统计量,为什么?学生也可以得出先求平均数,因为公式中需要平均值,这个问题可以使学生明确利用方差计算步骤。 教材P154例1在分析过程中应抓住以下几点: 1. 题目中“整齐”的含义是什么?说明在这个问题中要研究一组数据的什么?学生通过思考可以回答出整齐即波动小,所以要研究两组数据波动大小,这一环节是明确题意。 除采用教材中的引例外,可以选择一些更时代气息、更有现实意义的引例。例如,通过学生观看2004年奥运会刘翔勇夺110米栏冠军的录像,进而引导教练员根据平时比赛成绩选择参赛队员这样的实际问题上,这样引入自然而又真实,学生也更感兴趣一些。 2. 教材P154例1的设计意图: (1).例1放在方差计算公式和利用方差衡量数据波动大小的规律之后,不言而喻其主要目的是及时复习,巩固对方差公式的掌握。 (2).例1的解题步骤也为学生做了一个示范,学生以后可以模仿例1的格式解决其他类似的实际问题。 1. 教材P125的讨论问题的意图: (1).创设问题情境,引起学生的学习兴趣和好奇心。 (2).为引入方差概念和方差计算公式作铺垫。 (3).介绍了一种比较直观的衡量数据波动大小的方法--画折线法。 (4).客观上反映了在解决某些实际问题时,求平均数或求极差等方法的局限性,使学生体会到学习方差的意义和目的。 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |