2．菱形有什么性质？

1．什么样的平行四边形是菱形？

4．小结

　　 5．作业　

　　 活动与探究

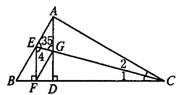
如下图在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F，四边形AEFG是菱形吗？

　　 过程：

　　 EA=EF(角平分线上的点到角两边的距离相等)

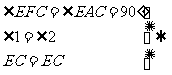　　 △EFC≌△EAC

EFGA是菱形．

　　 结论：四边形AEFG是菱形．

　　 备课资料

　　 参考例题

　　 [例1]请在括号中填写每一步推理根据．

已知菱形ABCD的边长为10，AC=12，求菱形ABCD的面积．

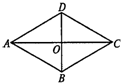　　 解：∵菱形ABCD(①)，

　　 ∴AO=CO，BO=DO(②)，

　　 ∠AOB=90°(③)．

　　 ∵AC=12(④)，

　　 ∴AO=6．

　　 ∵AB=10(⑤)，

　　 ∴BO=8(⑥)．

　　 ∴BD=2BO=16．

　　 ∴S_菱形ABCD=×16×12=96(⑦)．

　　 答案：①已知　 ②菱形对角线互相平分　 ③菱形的对角线互相垂直　 ④已知　 ⑤已知⑥　 勾股定理　 ⑦菱形面积等于对角线乘积的一半

　　 [例2]某中学有一块长为a米，宽为b米的矩形场地，计划在该场上修筑宽都为2米的两条互相垂直的道路，余下的4块矩形小场地建成草坪．

(1)如下图，请分别写出每条道路的面积．

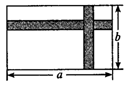
　　 (2)已知a：b=2：1，并且4块草坪的面积之和为312m²，试求原来矩形场地的长宽各为多少米？

　　 (3)在(2)的条件下，为进一步美化校园，根据实际情况，学校决定对整个矩形场地作如下设计(要求同时符合下述两个条件)

　　 ①在每块草坪上各修建一个面积尽可能大的菱形花圃(花圃各边必须分别与所在草坪的对角线平行)，并且其中有两个花圃的面积之差为13m²．

　　 ②整个矩形场地(包括道路、草坪、花圃)为轴对称图形．

　　 请你画出符合上述设计方案的一种草图(不必说画法与根据)，并求出每个菱形花圃的面积．

　　 解：(1)(2a+2b-4)m²

　　 (2)∵S_矩形场地=S_草坪+S_道路，设b=x，则a=2x，

　　 ∴x·2x-(2x+4x-4)=312．

　　 整理得x²-3x-154=0(解出这个方程即可解决问题．本题意图在于利用方程思想解决问题的意识．等学完一元二次方程后可继续解决这个问题)．解得x₁=14，x₂=-11(舍)．

　　 ∴b=14，a=28．

　　 矩形长28m，宽14m．

(3)设计如下图所示

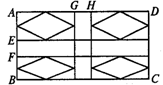
　　 说明：①AG=DH，这样保证整个场地为轴对称图形；②AE和FB的长度有赖于两个菱形面积之差为13m这一条件．

　　 下面分别计算AG和AE的长．

　　 设AG=x，则DH=x，∴x+2+x=28，∴x=13．

　　 设AE=y，则·y·13-(12-y)·13=13，解得y=7．

　　 ∴大花圃面积为×7×13=45.5(m²)．

　　 小花圃面积为×5×13=32.5(m²)．

3．随堂练习

2．应用举例：

　　 例3　　 议一议　　 做一做

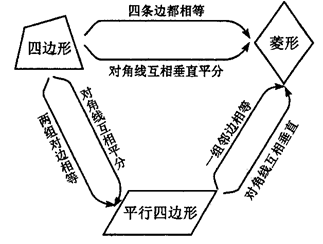
1．菱形的判定方法

　　 (1)定义：邻边相等的平行四边形

　　 (2)判定定理：对角线互相垂直的平行四边形　　　　　　 菱形

　　　　　　　　 四边相等的四边形

20.3 菱形的判定

2．预习正方形的判定

　　 板书设计

1．习题

　　 (引导学生归纳总结菱形的判定方法，通过课件演示逐渐得出下表．让学生从图形的变化中形象地看到被判定图形是四边形还是平行四边形，它们各要具备什么条件才是菱形，从中领悟到各种图形之间的内在联系)．