
2.正方形是怎样的特殊平行四边形?正方形,菱形有什么关系?正方形有什么性质?
1.矩形、菱形是怎样的特殊平行四边形,它们比平行四边形多些什么性质?
习题 14,15,16,17。
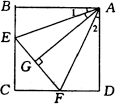 补例、如图,在正方形ABCD的BC、CD边上取E、F两点,使∠EAF=45°,AG⊥EF于G. 求证:AG=AB
补例、如图,在正方形ABCD的BC、CD边上取E、F两点,使∠EAF=45°,AG⊥EF于G. 求证:AG=AB
解析:欲证 AG=AB,就图形直观来看,应证Rt△ABE与Rt△AGE全等,但条件不够.
∠EAF=45°怎么用呢?显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.
证明:把 △AFD绕A点旋转90°至△AHB.
∵∠EAF=45°,∴∠1+∠2=45°.
∵∠2=∠3,∴∠1+∠3=45°.
又由旋转所得 AH=AF,AE=AE.
 ∴
△AEF≌△AEH.
∴
△AEF≌△AEH.
师生共同总结,归纳得出正方形的判定方法,同时展示下图,通过直观感受进一步加深理解正方形判定方法的应用。

通过练习进一步巩固正方形的判定方法的应用。
3、连结AB﹑BC﹑CD﹑DA.
则四边形ABCD就是所要画的正方形.
证明:∵AO=CO,BO=DO
四边形ABCD是平行四边形。
又∵AC=BD, ∴平行四边形ABCD是矩形。
∵AC⊥BD
∴平行四边形ABCD是菱形。
∴四边形ABCD是正方形(四边形既是矩形又是菱形,则四边形是正方形)。
说明:由学生分析画法,在证明过程中让学生逐一说出判断理由,以加深对正方形的判定方法的认识.
2、过点O画AC的垂线,并分别在AC的两侧取OB=OD=15cm。
2、正方形判定条件的应用
[例1]判断下列命题是真命题还是假命题?并说明理由。
(1) 四条边相等且四个角也相等的四边形是正方形;
(2) 四个角相等且对角线互相垂直的四边形是正方形;
(3) 对角线互相垂直平分的四边形是正方形;
(4) 对角线互相垂直且相等的四边形是正方形;
(5) 对角线互相垂直平分且相等的四边形是正方形。
师生共析:
(1) 是真命题。因为四条边相等的四边形是菱形,又四个角相等,根据四边形内角和定理知每个角为90°,所以由有一个角是直角的菱形是正方形可以判定此命题是真命题。
(2) 真命题。四个角相等可知每个角都是直角,是矩形,由对角线互相垂直可判定这个矩形是菱形,所以根据是矩形又是菱形的四边形是正方形,可判定其为真。
(3) 假命题。对角线平分的四边形是平行四边形,对角线垂直的四边形是菱形,所以它不一定是正方形。如下图,满足AO=CO,BO=DO且AC⊥BD但四边形ABCD不是正方形。


(4) 假命题。它可能是任意四边形。如上图,AC⊥BD且AC=BD,但四边形ABCD不是正方形。
(5) 真命题。
方法一,对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形,对角线垂直的平行四边形是菱形,所以是矩形又是菱形的四边形是正方形。可判定其为真。



 方法二,对角线平分
平行四边形
方法二,对角线平分
平行四边形

 对角线垂直
对角线垂直


 平行四边形
平行四边形
 对角线相等
对角线相等
方法三,由对角线互相垂直平分可知是菱形,由对角线平分且相等可知是矩形,而既是菱形又是矩形的四边形就是正方形。
总结:通过辨析,掌握判定正方形的各种方法和思路,从题中所给各种不同条件出发寻找命题成立的判定依据,以便灵活应用。
 [例2]如下图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°,试说明EF=BE+DF。
[例2]如下图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°,试说明EF=BE+DF。
师生共析:要证EF=BE+DF,如果能将DF移到EB延长线或将BE移到FD延长线上,然后证明两线段长度相等。此时可依靠全等三角形来解决。
像这种在EB上补上DF或在FD补上BE的方法叫做补短法。
解:将△ADF旋转到△ABC,则△ADF≌△ABG
∴AF=AG,∠ADF=∠BAG,DF=BG
∵∠EAF=45°且四边形是正方形,
∴∠ADF﹢∠BAE=45°
∴∠GAB﹢∠BAE=45°
即∠GAE=45°
∴△AEF≌△AEG(SAS)
∴EF=EG=EB﹢BG=EB﹢DF
[例3]画一个正方形,使它的对角线长为30,并说明画法的依据。
画法:1、画线段=30cm,取AC的中点O。
1、探索正方形的判定条件:
学生活动:四人一组进行讨论研究,老师巡回其间,进行引导、质疑、解惑,通过分析与讨论,师生共同总结出判定一个四边形是正方形的基本方法。
(1)直接用正方形的定义判,即先判定一个四边形是平行四边形,若这个平行四边形有一个角是直角,并且有一组邻边相等,那么临就可以判定这个平行四边形是正方形;
(2)先判定一个四边形是矩形,再判定这个矩形是菱形,那么这个四边形是正方形;
(3)先判定四边形是菱形,再判定这个菱形是矩形,那么这个四边形是正方形。
后两种判定均要用到矩形和菱形的判定定理。矩形和菱形的判定定理是判定正方形的基础。这三个方法还可写成:有一个角是直角,且有一组邻边相等的四边形是正方形;有一组邻边想的相等的矩形是正方形;有一个角是直角的菱形是正方形。
上述三种判定条件是判定四边形是正方形的一般方法,可当作判定定理用,但由于判定平行四边形、矩形、菱形的方法各异,所给出的条件各不相同,所以判定一个四边形是不是正方形的具体条件也相应可作变化,在应用时要仔细辨别后才可以作出判断。
4、怎样判断一个平行四边形是矩形、菱形?
议一议:你有什么方法判定一个四边形是正方形?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com