
2.思考题 已知正方形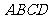 的边长为4,
的边长为4,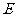 为
为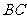 边上一点,且
边上一点,且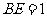 ,
,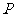 为
为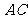 上一点,求
上一点,求 的最小值
的最小值
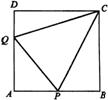
2.补充练习:如图4,已知正方形ABCD,延长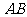 到
到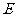 ,
,
连结 ,作
,作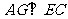 于
于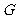 ,
,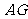 交
交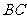 于
于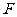 ,求证:
,求证: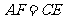 .
.
小结:
2.正方形的性质
因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结).
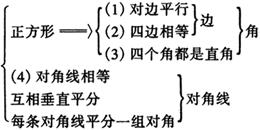
正方形性质定理1:正方形的四个角都是直角,四条边相等.
正方形性质定理2:正方形的两条对角钱相等并且互相垂直平分,每一条对角线平分一组对角.
说明:定理2包括了平行四边形,矩形,菱形对角钱的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全.
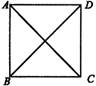 例题讲解:例4 如图3,
例题讲解:例4 如图3,
|
设问:矩形和菱形都是特殊的平行四边形,那么更加特殊的平行四边形是什么图形?它又有什么特殊性质呢?这一堂课就来学习这种特殊的图形--正方形(写出课题)
1.正方形的定义:有一组邻边相等,有一个角是直角的平行四边形叫做正方形.
设问:正方形从定义看,它既是矩形又是菱形。哪么它又有什么性质呢?
2.说明平行四边形、矩形、菱形的内在联系.
1.让学生叙述平行四边形、矩形、菱形的定义和它们的特殊性质.
图3
(1)判定一个四边形为正方形的基本方法:定义法,矩形菱形法.
(2)正方形的性质较多,在证题时要灵活应用.
2. 思考题:已知如图3正方形
思考题:已知如图3正方形 的边长为1,
的边长为1, 、
、 上都有一点
上都有一点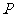 、
、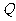 ,如果△
,如果△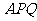 周长为2,求
周长为2,求 度数.
度数.
2. 四个角都是直角.
因此,正方形可以看作为:有一个角是直角的菱形;有一组邻边相等的矩形.
这些实际上就是判定正方形的方法.
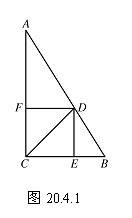 例 如图20.4.1,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.求证: 四边形CFDE是正方形.
例 如图20.4.1,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.求证: 四边形CFDE是正方形.
分析 要证明四边形CFDE是正方形,可以先证四边形CFDE是矩形,然后再证有一组邻边相等;也可以先证四边形CFDE是菱形,然后再证有一个角是直角.
证明 ∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
又∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
正方形的判定方法:提问:
1:对角线相等的菱形是正方形吗?
2:对角线互相垂直的矩形是正方形吗?为什么?
3:对角线垂直且相等的四边形是正方形吗?为什么?
4:四条边都相等的四边形是正方形吗?为什么?
5:说“四个角相等的四边形是正方形”对吗?
我们已经知道,正方形是一个中心对称图形,也是一个轴对称图形,具有如下的性质:
1. 四条边都相等;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com