3．证明：∵四边形ABCD是梯形．

　　 ∴AD∥BC，

　　 ∴∠A与∠B互补，

　　 ∵∠A与∠C互补，

　　 ∴∠B=∠C．

　　 ∴梯形ABCD是等腰梯形．

1．解：FC=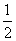(BC-AD)=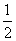(4-2)=1，

　　 DC=．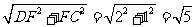

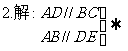　　 四边形ADEB是平行四边形

　 AD=DE=6，AD=BE=5．

　　 ∵四边形ABCD是等腰梯形，

　　 ∴AB=CD=6．

　　 EC=BC-BE=8-5=3．

　　 ∴△CDE的周长为6+6+3=15．

5．作业　 习题

　　 活动与探究

如下图，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A点开始沿AD边以1cm/s的速度向D运动，动点Q从C点开始沿CB边以3cm/s的速度向B运动，P、Q分别从A、C同时出发，当其中一点到端点时，另一点也随之停止运动．设运动时间为ts，t分别为何值时，四边形PQCD是平行四边形，等腰梯形？

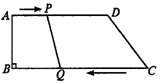
　　 过程：这是一个探索性的题，题中涉及了平行四边形的判定，等腰梯形的性质及判定，让学生在充分理解题的情况下，进行探讨．

　　 结果：解：∵AD∥BC，

　　 ∴只要PD=CQ，四边形PQCD是平行四边形．

　　 这时，根据题意有

　　 24-t=3t，解得t=6(s)．

　　 同理可知：只要PQ=CD，PD≠CQ四边形PQCD是等腰梯形．

　　 过P、D分别作BC的垂线，交BC于点E、F，则四边形PEFD是矩形，△PQE≌△DCF．

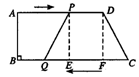　　 ∴PD=EF，CF=QE=2．

　　 ∴24-t=3t-2×2，解得t=7(s)．

　　 因此，t为6时，四边形PQCD是平行四边形，t为7时，四边形PQCD是等腰梯形．

　　 习题详解

　　 习题19．3

4．小结

3．随堂练习

2．应用举例

　 　例2

　　 补充题：画法一、画法二、画法三．

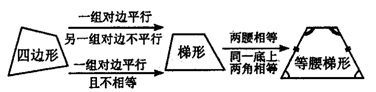
1．等腰梯形的判定方法

　　 (1)两腰相等的梯形是等腰梯形．

　　 (2)同一底上两个角相等的梯形是等腰梯形．

　　 习题

　　 板书设计

20.5 等腰梯形的判定

　　 (与学生共同梳理，总结梯形的判定方法及添加辅助线解决有关梯形问题常用方法．同时演示课件，让学生加深理解并记忆)．

　　 等腰梯形的判定方法：

　　 (1)两腰相等(定义)

　　 (2)同底上的两个角相等(判定定理)

　　 梯形的画法：画出符合条件的梯形，通常先要“分析”，借助辅助线找出可以画出的部分图形(等腰三角形，直角三角形等)

　　 梯形中常用的四种辅助线的添法(如下图)：

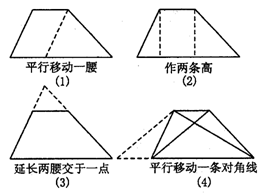
2．补充练习．

　　 (1)等腰梯形与等腰三角形有哪些联系？

　　 答：延长一个等腰梯形的两腰，可以得到一个等腰三角形；过一个等腰三角形腰上一点作底边的平行线，可以得到一个等腰梯形．

　　 (2)有两个内角是70°的梯形一定是等腰梯形吗？为什么？

　　 答：是等腰梯形，理由是：

　　 这两个70°的内角的位置仅有三种可能：

　　 ①相邻：顶点是同一条腰的两个端点．

　　 ②相邻：顶点是同一底边的两个端点．

　　 ③相对．

　　 当顶点是一条腰的两个端点时，两个角应该是互补的；两角相对时，可以推得此时的四边形是平行四边形．因此，这两个70°的内角只能是同一底上的两个内角，因此这个梯形是等腰梯形．