
2.等腰梯形有何特殊性质?
1.什么样的几何图形是梯形?什么样的几何图形是等腰梯形?
1.答案:AB=4 S梯形ABCD=14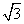 .
.

 BD=4
BD=4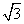 ,
,
∴BC=BD=4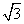 (cm).
(cm).
∵四边形ABCD是梯形,且AD∥BC,
∴∠B=180°-∠A=60°,
又AB=4.
∴梯形的高h=2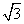 .
.
∴S梯形ABCD=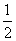 (AD+BC)·h=
(AD+BC)·h=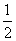 (4+4
(4+4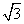 )·2
)·2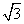 =12+4
=12+4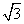 (cm)2.
(cm)2.
2.已知在梯形ABCD中AD∥BC,BC=BD,AD=AB=4cm,∠A=120°,求梯形ABCD的面积.
1.在梯形ABCD中,AD∥BC,AD=5,BC=9,∠B=60°,求AB的长和梯形ABCD的面积.
9.解:EF=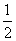 (AD+BC),
(AD+BC),
平移CD到AM,交EF于点N,
则四边形ADCM是平行四边形,且N是MA的中点.
∴EN是△ABM的中位线.
∴EN=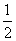 BM,
BM,
EF=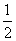 BM+FN=
BM+FN=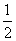 BM+
BM+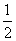 (AD+NC)
(AD+NC)
=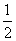 (AD+BC).
(AD+BC).
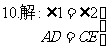
 Rt△ODA≌Rt△OEC
Rt△ODA≌Rt△OEC
 ∠DAO=∠ECO,DO=EO
∠DAO=∠ECO,DO=EO
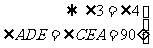
 ∠ADE=∠CED,
∠ADE=∠CED,
同理可证∠DAC=∠ECA.
又∵四边形内角和为360°,
∠DAC+∠ADE=180°.
∴DE∥AC.
又∵AD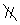 EC.
EC.
∴四边形ADEC是梯形.
又AD=EC,
∴四边形ACED是等腰梯形.
梯形的高h=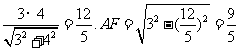 .
.
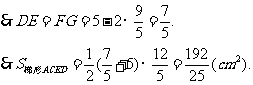
备课资料
8.6个等腰梯形.
7.证明:AD∥BC
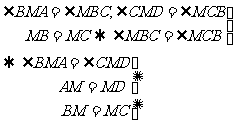
 △ABM≌△DCM
△ABM≌△DCM
 AB=CD
AB=CD
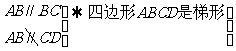
 梯形ABCD是等腰梯形.
梯形ABCD是等腰梯形.
6.证明:∵四边形ABCD是等腰梯形,
∴AD∥BC,∠B=∠DCB.
∴∠CDE=∠DCB.
∵CD=CE,
∴∠E=∠CDE.
∴∠B=∠E.
4.解:S横截面=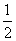 ×20×1.5+
×20×1.5+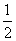 (2.65+1.5)×(40-20)+2.65(60-40)+(2.65+1.9)(80-60)+
(2.65+1.5)×(40-20)+2.65(60-40)+(2.65+1.9)(80-60)+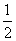 (100-80)×1.9=174(m).
(100-80)×1.9=174(m).
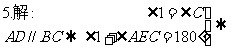 ∠C+∠AEC=180°
∠C+∠AEC=180°
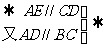 四边形AECD是平行四边形
四边形AECD是平行四边形 AD=EC,AE=CD.
AD=EC,AE=CD.
△ABE的周长=梯形ABCD的周长-2AD=29-2×5=19.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com