
20.(7’)比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴出发,到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议,蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达,已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度。
18. (6’)先化简,再求值: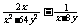 ,其中x=1,
,其中x=1, .
.
 19.(7’)△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm,求AC.
19.(7’)△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm,求AC.
17. (6’)解方程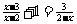
16.已知一个样本1,3,2,5,x,它的平均数是3,则这个样本的方差为( )
A.2 B.3 C.4 D.5
15.矩形ABCD的对象线AC,BD相约于点O,且∠AOB=60°,AB=8CM,则AC长为( )
 A.16CM B.8CM C.8
3CM D.24CM
A.16CM B.8CM C.8
3CM D.24CM
|
13. 若
中x,y值都扩大3倍,则分式的值( )
若
中x,y值都扩大3倍,则分式的值( )
A.扩大3倍 B.不变 C.缩小3倍 D.扩大9倍
|
|
 的图象上的一个点的坐标是( )
的图象上的一个点的坐标是( )

 A.(3,1) B.(-3,1) C.(3, ) D.( ,3)
A.(3,1) B.(-3,1) C.(3, ) D.( ,3)
25、解:(1)在等腰梯形ABCD中,AD=BC=10 ……1分
又 A(0,8)
∴ OA=8 ……2分
∴ OD= =6
……3分
=6
……3分
∴ D(-6,0) ……4分
 (2)作BH⊥DE于H,过B点作BE∥AC交x轴于点E
(2)作BH⊥DE于H,过B点作BE∥AC交x轴于点E
∵ AB∥CE, BE∥AC
∴ ABEC是平行四边形 ……5分
∴ AB=CE,BE=AC
又 AC=BD
∴ BE=BD
而AC⊥BD, AB∥CE
∴ ∠DPC=∠DBE=90°
∵ BH⊥DE
∴ BH= DE=
DE= (DC+CE)=
(DC+CE)= (DC+AB)=
(DC+AB)= ×34=17
……6分
×34=17
……6分
∵ BC=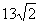
∴ CH= =7
=7
∴ OH=AB=CE=HE-HC=17-7=10
∴ B(10,17) ……7分
∴ 过B点的反比例函数的解析式为:
y=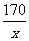 ……8分
……8分
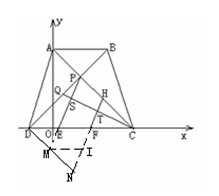 (3)过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I
(3)过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I
易证四边形EFIM和四边形MNHP是平行四边形
∴MI=EF=DE,MN=PH ……9分
又∵∠EDM=∠IMN,∠DEM=∠EFI=∠MIN
∴△EDM≌△IMN
∴DM=MN ……10分
∵∠PDM=∠CPQ=90°,∠DPM=∠QCP=90°-∠SPC
由(2)知:∠BDC=45°,而∠DPC=90°,
∴PD=PC
∴△PDM≌△CPQ ……11分
∴DM=PQ=PH∴ =1
……12分
=1
……12分
(注:不同的解法参照此标准给分)
24、解:(1)1 ……2分
(2)1 ……4分
(3)如图3, =1
=1
过点P作PN⊥AB,垂足N在AB的延长线上,PN交CQ于点M ……5分
 在正方形ABCD中,AB∥CD
在正方形ABCD中,AB∥CD
∴∠PMQ=∠N=∠CBN=90° ……6分
∴CBNM是矩形
∴CM=BN ……7分
易证△CMP是等腰直角三角形
∴PM=CM=BN ……8分
又∠1=∠PBN=90°-∠BPN
∴△PMQ≌△BNP(ASA) ……9分
∴PQ=PB
∴ =1
……10分
=1
……10分
如图4 , =1
=1
过点P作PN⊥AB,垂足N在BA的延长线上,PN的延长线交CQ于点M
在正方形ABCD中,AB∥CD
 ∴∠PMC=∠PNB=∠CBN=90°
……6分
∴∠PMC=∠PNB=∠CBN=90°
……6分
∴CBNM是矩形
∴CM=BN ……7分
易证△CMP是等腰直角三角形
∴PM=CM=BN ……8分
又∠1=∠2=90°-∠BPN
∴△BNP≌△PMQ (ASA) ……9分
∴PB=PQ
∴ =1
……10分
=1
……10分
23、解:(1)月销售额在15万元的人最多, ……2分
月销售额处于中间的是18万元, ……4分
平均月销售额是20万元. ……6分
(2)因为平均数、中位数和众数分别为20万元、18万元和15万元,而
平均数最大,所以可以估计月销售额定为每月20万元是一个较高的目标.
……8分
(3)如果想让一半左右的营业员都能达到目标而得到奖励,月销售额可定为每月18万元(中位数),因为月销售额在18万元以上(含18万元)的人数有16人,占总人数的一半左右,所以可以估计,月销售额定为18万元,将有一半左右的营业员获得奖励.
……10分
22、解:(1)图象的另一支在第三象限. ……1分
∵ 图象在一、三象限
∴ 5-2m>0
∴ m< ……2分
……2分
(2)∵ m<
∴ m-4<m-3<0 ……3分
∴ b1 <b2 ……5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com