(二)关注应用数学知识解决问题的考查

数学知识不仅来源于数学内部系统，还来源于社会生活实际，同时又被应用于实践。关注数学与生活现实的联系有助于提高学生学习的积极性，有助于培养学生的应用意识与解决问题的能力，有助于增进他们对数学的理解与认识，是《课程标准》所倡导的基本理念。从实验区的数学试卷中我们欣喜地看到，各地对此都非常重视，都保证了有较高的分值来设计数学与生活现实相联系的试题。同时，在试题的素材中体现教育价值也成为不少试卷的共同特征。

例21　 (泉州市) 某校初一、初二两年段学生参加社会实践活动，原计划租用48座客车若干辆，但还有24人无座位坐．

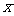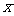(1)设原计划租用48座客车辆，试用含的代数式表示这两个年段学生的总人数；

(2)现决定租用60座客车，则可比原计划租48座客车少2辆，且所租60座客车中有一辆没有坐满，但这辆车已坐的座位超过36位．请你求出该校这两个年段学生的总人数．

答案　 (1)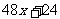；(2)648.

评析　 本题主要考查学生能否用数学符号和代数式表示一个简单的现实情境，并在此基础上应用数学知识进行求解，得到原问题的答案。

例22　 (泉州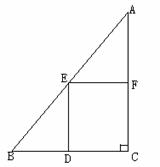市)如图是某居民小区的一块直角三角形空地ABC，其斜边AB=100米，一直角边AC=80米．现要利用这块空地建一个矩形停车场DCFE，使得D点在BC边上，E、F分别是AB、AC边的中点．

(1)求另一条直角边BC的长度；

(2)求停车场DCFE的面积；

(3)为了提高空地利用率，现要在剩余的△BDE中，建一个半圆形的花坛，使它的圆心在BE边上，且使花坛的面积达到最大.请你在原图中画出花坛的草图，求出它的半径(不要求说明面积最大的理由)，并求此时直角三角形空地ABC的总利用率是百分之几(精确到1%)？

答案　 (1)60米；(2)1200米²；(3)半径为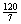米，总利用率约为69%.

评析　 本题是贴近社会生活的应用题，考查不等式和函数的思想，让学生在经历自主探索的思维过程的基础上发现有意义的结论，有较大的思考的空间，能够为具备相应知识水平的学生展现其探究能力提供机会。

例23 (苏州市)为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE。(精确到0.1m)

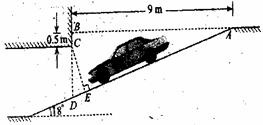
　 　答案　 2.3m

评析　 在经济高速发展、生活率先进入“小康”的苏州，这样一个现实的问题具有很强的地域特色。对于该地区参加中考的学生而言，感受最深的不再是某些数学应用题中“应用”光环下人为编造的痕迹，而是生活中经常出现的问题很自然地反映到了数学考试上。

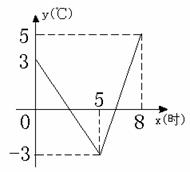例24　 (宁夏省)春、秋季节，由于冷空气的入侵，地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.

　 　某种植物处在气温0℃以下持续时间超过3小时，即遭受霜冻灾害，需采取预防措施.下图是气象台某天发布的该地区气象信息，预报了次日0时-8时气温随时间变化情况，其中0时-5时，5时-8时的图像分别满足一次函数关系.请你根据图中信息，针对这种植物判断次日是否需要采取防霜冻措施，并说明理由.

答案　 不需要采取防霜冻措施，理由略。

评析　 本题将数学问题生活情景化，合理设置探索性问题空间，拉近数学与学生学习、生活的距离，让学生感受到数学的真实性，感受到数学与社会，数学与生活的关系。题中涉及图像的解读，一次函数解析式的确定，运用一次函数知识解释实际问题，同时又能利用三角形全等和相似来解决这一实际问题，充分体现代数与几何知识的有机结合。

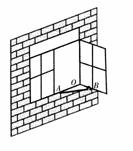例25　 (山西省) 如图，一扇窗户打开后用窗钩AB可将其固定，这里所运用的几何原理是(　　 )

A、三角形的稳定性　　　　

B、两点之间线段最短

C、两点确定一条直线　　　

D、垂线段最短

答案　 A

评析　 本题以现实生活情景为背景，加入了实物图，给学生以亲切感，不会让学生对试卷感到“望而生畏”，让学生感受到身边处处有数学，身边处处用数学。试题淡化对某些特殊解题技巧的使用，注重对数学核心知识的理解和应用能力的考查，能够较好反映学生运用数学知识的灵活程度。

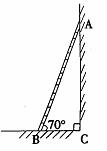例26　 (泉州市)如图，一架梯子AB斜靠在一面墙上底端B点与墙角C的距离BC为1米，梯子与地面的夹角为70°，求梯子的长度(精确到0.1，供选用的数据：sin70°=0.9397,cos70°=0.3420,tan70°=2.7475,cot70°=0.3640)

答案　 2.9米

评析　 本题考查学生运用数学知识分析、解决简单实际问题的能力.本题取材于学生熟悉的生活实际，解决这类题目的难度虽不大，但有利于引导学生关注生活中的数学，关注身边的数学，培养他们从实际问题中抽象出数学模型的能力，促进学生形成学数学、用数学、做数学的良好意识．

例27　 (南京市) 某水果店有200个菠萝，原计划以2.6元/千克的价格出售，现在为了满足市场需要，水果店决定将所有的菠萝去皮后出售。以下是随机抽取的5个菠萝去皮前后相应的质量统计表：(单位：千克)

(1)计算所抽取的5个菠萝去皮前的平均质量和去皮后的平均质量，并估计这200个菠萝去皮前的总质量和去皮后的总质量。

(2)根据(1)的结果，要使去皮后这200个菠萝的销售总额与原计划的销售总额相同，那么去皮后的菠萝的售价应是每千克多少元？

答案　 (1)去皮前1.2千克，去皮后0.78千克。估计200个菠萝去皮前后总质量分别为240千克和156千克；(2)4元/千克。

评析　 本题以菠萝去皮前后的质量变化为情景，将统计问题与方程问题有机地结合起来，情景合乎生活逻辑，问题表述明白易懂，易于理解，试题呈现的可读性较好，命题者设计自然、合理，难度适当，能有效地考查学生对样本估计总体的数学思想及相关知识的掌握。

例28　 (安徽省)两人要去某风景区游玩，每天某一时段开往该风景区有三辆汽车(票价相同)，但是他们不知道这些车的舒适程度，也不知道汽车开过来的顺序，两人采用了不同的乘车方案：

　　 甲无论如何总是上开来的第一辆车，而乙则总是先观察后上车，当第一辆车开过来时，他不上车，而是仔细观察车的舒适状况。如果第二辆车的状况比第一辆好，他就上第二辆车；如果第二辆车不比第一辆好，他就上第三辆车。

　　 如果把这三辆车的舒适程度分为上、中、下三等，请尝试解决下列问题：

　　 (1)三辆车按出现的先后顺序共有几种不同的可能？

(2)你认为甲、乙两人采用的方案，哪一种方案使自己乘坐上等车的可能性大？为什么？

答案　 (1)用A、B、C分别表示三辆车的舒适程度上、中、下三等，对车辆出现的先后顺序作出：按照从左向右的顺序依次写出先、后出现的车辆.所有可能的情形为：ABC、ACB、BAC、BCA、CAB、CBA，共计6种可能

(2)能使甲乘坐上等车的所有情形是ABC、ACB；能使乙乘坐上等车的所有情形是BAC、BCA、CAB.因为6种情形出现的可能性相等，所以甲坐上等车的概率是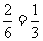，乙坐上等车的概率是.

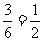评析　 本题是一道利用概率知识来解决决策问题的优秀试题，它有如下三点有价值的地方：(1)学习数学要养成一种理性思维的习惯，遇到一个问题，不能凭经验决策，也不能凭直觉决策(尽管二者确实是作出决策的一个重要参考)，而应当增加理性的分析与计算，本题就蕴含了这一思想，将数学的理性精神通过中考试题对学生形成潜移默化的影响；(2)问题情景自然合理，这是应用性问题设计的一个重要方面，本题做得很成功；(3)本题的设计回避了对问题解决的思路作出任何暗示，需要学生根据实际问题的分析来发现其中所隐含的数学模型，这是一种做数学的要求，对于压轴题来讲，这一点是非常需要的，这也是考查能力的有效做法。

(六) 学会分析方法：

如，函数中的待定系数

　　　 已知　　　

转化点　　　　　　　　　　 文字--符号

的坐标　　　　　　　　　　 几何条件

点的坐标　 已知的等量关系

代入函数　　　　　　　　 　　用系数的代数

解析式　　　　　　　　　　　 式表示 …

　　　　　 构造关于系数 ( 如，a、b ) 的方程

(如， 定c 待a 、b )　　 待定的系数越少越好

　　　　　　 定系数 ( 如，a、b、c ) 的值

　 求函数解析式(如，y = ax² + bx + c ( a ≠ 0 ) )

(五) 构造函数解析式中待定系数的方程的方法：

　　 1. 利用函数的定义(隐含它们最高项的系数 ≠ 0)

　 　　　　　　　　　　- 一次函数 　x的最高指数 = 1

　 　　　　函数定义 -- 二次函数 　x的最高指数 = 2　

　　　　　　　　　　　 - 反比例函数　 x的指数 = - 1

2. 函数图象上一点坐标满足函数解析式(注意转化点的坐标)

　　　 　[待定系数法构造关于“系数”方程的主要方法]

3. 利用题目的条件直接构造方程　

　[用含有待定系数的代数式表示点的坐标]

如，二次函数图象的顶点在x轴上(令 y = 0，Δ ≥ 0 ) 　例35

4. 利用几何中公式、定理做为等量关系构造方程　　　　 　　例49

　　　 [用含有待定系数的代数式表示线段长]

　　　　　 如，面积公式、勾股定理、相似三角形对应边成比例　 等

5. 利用图形中的等量关系构造方程　 如， 线段和差　 等　 例25

(四) 对“点的坐标代入函数解析式”的认识

　　 1. 将已知点的坐标代入函数解析式，构造有关系数的方程； 例33(1)(2)

2. 已知函数解析式及其图象上一点的某坐标，求这点的坐标 例33(3)

　　　 [将点的坐标代入函数解析式，构造这点另一坐标的方程]

3. 已知函数解析式及图象上一点(a，b)，但a，b未知，求点坐标 例15(7)

[将点的坐标代入函数解析式，构造关于a，b的方程]

[还须一个条件，构造关于a，b的另一个方程]

4. 函数解析式中有待定系数k，点的某坐标a不知道，求函数解析式及点的坐标

[将点的坐标代入函数解析式，构造关于a，k的方程] 　　　　例33(4)

5. 用函数解析式中待定系数a、b表示点的坐标，将点的坐标代入另一函数解析式，构造关于a，b的方程　 　　　　　　　　　　　　　　　　　

6. 求两个已知函数图象的交点坐标.

[解这两个函数解析式联立的二元一次方程组]

例30(2)(山东省潍坊课改实验区2004)若M(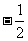，y₁)、N(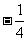，y₂)、P(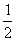，y₃)三点都在函数y=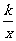(k < 0)的图像上，则y₁ 、y₂ 、y₃ 的大小关系为　 (　　 )　　　　　　　　　　　　 　　　　

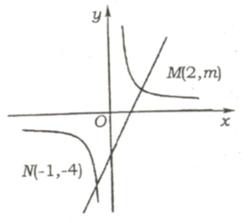(A)y₂ >y₃ >y₁(B)y₂ >y₁ >y₃

(C)y₃ >y₁ >y₂ (D)y₃ >y₂ >y₁

3. 反比例函数的应用　 　　　　例31

4. 相关的综合题　　　 　　　例32　　

例32 (2)(贵阳市课改实验区)如图，一次函数y= ax + b的图像与反比例函数y=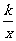的图象交于M、N两点

　　　　 1)求反比例函数和一次函数的解析式；

　2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。

二次函数

[基本题型，基本方法]

1.　　 二次函数解析式与它图象上的点[用方程思想]　 例33--例36

二次函数解析式的两种形式(注意隐含条件、优选解析式)：

y = ax² + bx + c ( a ≠ 0 )

y = a(x – h)² + k ( a ≠ 0 )　　 (已知对称轴、顶点)

例33 (4)　 抛物线 y = 2x² + bx – 5 过点A ( - 2, y_A )，则 y_A = 　　　　　

(6) 二次函数 y = ax² + bx + c的图象与 x 轴交于点A ( - 3, 0 )，

对称轴x = -1，顶点C到x轴的距离为2，则设 y = 　　　　　　　,

得方程为　　　　　　 ，解得　　　　　　 ，

此函数解析式为 　　　　　　　　　　.　 (优选顶点式)

2. 二次函数中的数形结合[用数形结合思想](依形判数，由数思形)

　 看二次函数的图象：

一看与 y 轴交点 ( 0, c )， 定常数项 c. 　　　例38

　　　　　 二看图象的开口方向定 a 的符号：　　 　　　例37(1)(2)

开口向上　 a ＞ 0

　　　　　　　　　　 开口向下　 a ＜ 0

　　 　　三看抛物线与 x 轴的相对位置：　　　　　　 例37(4)　 例41

　　　　　　　　 抛物线与 x 轴有两个交点，⊿ ＞ 0；

　　　　　　　　 抛物线与 x 轴有一个交点，⊿ ＝ 0；

　　　　　　　　 抛物线与 x 轴无交点，　　 ⊿ ＜ 0.

　　　 四看抛物线对称轴与 y 轴的相对位置：　 　　　例40(1)

　　　　　　　　　　 对称轴在 y 轴的左侧，a 、b 同号：

　　　　　　　　　　 对称轴在 y 轴的右侧，a 、b 异号.

　　　　 　　五看图象的走向定函数的增减性：(以对称轴为界)　

　　　　　　　　　　 左低右高　 y 随 x 增大而增大,　　　　　　　　　　　　　　　　　　　

左高右低　 y 随 x 增大而减小　

　　　　　 六看部分图象对应的取值范围： 　　　　　　　例37(3) 　　　　　　　　

　 (图象端点向 x 轴引垂线，由垂足对应的数看 x 的取值范围)

　 (图象端点向 y 轴引垂线，由垂足对应的数看 y 的取值范围)　　

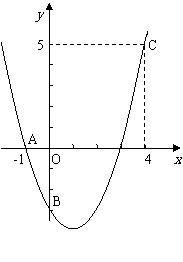例38(沈阳市2004)如图，二次函数y=ax²+bx+c的图象经过A、B、C三点.

(1)观察图象写出A、B、C三点的坐标，并求出此二次函数的解析式；

(2)求出此抛物线的顶点坐标和对称轴。

画二次函数图象　　 (略)

3．图形的移动(翻转，平移，旋转)　　 　　　　　　　例42--例44

例42(1)(山东省潍坊课改实验区2004)抛物线y=ax²+bx+c如图所示，则它关

于y轴对称的抛物线的解析式为　　　　　 。

4. 二次函数的应用　 　　　　　例45，例46

例45 (吉林省2004)如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距.某项研究表明，一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据：

(1)　　　　　 求出h与d之间的函数关系式(不要求写出自变量d的取值范围)：

(2)　　　　　 某人身高为196cm，一般情况下他的指距应是多少？

5. 相关的综合题 　　　　　　　　　　　　　　　　例47--例52 　

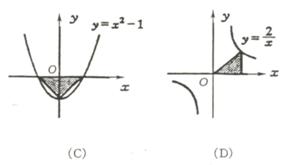
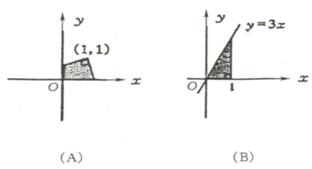
例51下列图中阴影部分的面积与算式|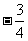|+(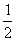)² + 2^-1的结果相同的是　　 (　　　 )

二看图象的位置定函数的增减性：　

(三)对三类函数的理解(数形结合)

[知识要点]

函数	一次函数	反比例函数	二次函数
解析式	y = kx + b (k ≠o)	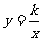(k ≠o)	y = ax2 + bx+c ( a ≠ 0 )
结构	结构　　　　 　形状	结构　 直线	结构　 双曲线	结构　 抛物线
形状 加条件 结构	不平行于坐标轴的直线　　　　　　　　　　　 结构	加条件 　　　 结构	对称轴平行y轴 　 　　　　结构
系数	定　　 向	k　　 定向	k 　　定位置	a符号 　开口方向 |a| 　　　开口大小
定　　 轴	--	--	ab符号　 　　 对称轴位置
定　　 点 (1)与y 轴的交点(交点恰在 y 轴上) 　 　 (2)抛物线 的顶点	b　 定点　　 　　 　　(0, b) 常数项= 与y轴交点纵坐标 (常数项1　 = 常数项2)	--	c　 定点 　　　 (0, c) 常数项= 与y轴交点纵坐标 ( 常数项1 = 常数项2 )
a、b、c　 　　　 定点 (-，)
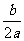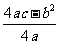定增减性	k ＞ 0,y　 随 x　 　 增大而增大 k ＜ 0,y 　随 x　 　 增大而减小	k ＞ 0,y　 随 x 　 增大而减小 k ＜ 0,y　 随 x 　 增大而增大	略
令y = 0的根x	定　　 点 　 　 与x 轴的交点	令y = 0的根x 定点 　 (x ，0)	--	令y = 0的两根x1,x2　　　　　　　　 定点 (x1，0)，(x2，0)

一次函数

[基本题型，基本方法]

1. 一次函数的解析式与它图象上的点[用方程思想]

　 1)求函数解析式 　　　　　　　例15(1)(3)(4)(6)

　　　　　 [将点的坐标代入解析式，是构造关于“系数”方程的主要方法]

　　　　　 [转化点的坐标是求函数解析式的重要方法]

求函数解析式的步骤：

　　　 一设 (优选函数解析式，尽量用概念定系数，使待定的系数越少越好)

　　　 二构 (将点的坐标代入解析式，构造待定系数的方程或方程组，)

　 　　　　(用已知等量关系或几何条件，构造待定系数的方程或方程组)

　　　 三解 (解方程或方程组)

　　　 四回代(将解出来的系数代入所设的函数解析式)

例15(3) 若一次函数图象过A (2, -1)和B两点，其中点B是另一条直线y =﹣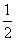x + 3与y 轴的交点，求这个一次函数的解析式.　 (定b待k)

　2)求点的坐标 　　　　　　　　例15(2)(4)(5)(6)(7)

例15(7) 已知 y = 3x – 2 的图象经过点( a，b )，且 a + b = 6，求a、b的值.

2. 一次函数中的数形结合[用数形结合的思想](依形判数，由数思形)

看一次函数的图象　

一看与 y 轴交点 ( 0, b )， 定常数项 b。　　　　　　 例16(1)

　 　　　　二看图象的走向定 k的符号：左低右高　 k ＞ 0 　　

左高右低　 k ＜ 0　　　　　　　 同步练习册　 八册下　 P17.3

　　　　　 三看图象的走向定函数的增减性：　　　　　　　 　　例16(2)　

　　　　　　　　　　　　　　　　 左低右高　 y 随 x 增大而增大,　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　 左高右低　 y 随 x 增大而减小

　　　　　 四看图象所在象限定k, b 符号：(略)　 同步练习册　 八册下　 P17.1(2)

画一次函数的图象　

例17 新课程标准P36 例11　

　　 填表并观察下列两个函数的变化情况：

(3)　　 在同一个直角坐标系中画出上面两个函数的图象，比较它们有什么不同；

(4)　　 当 x 从1开始增大时，预测哪一个函数的值先到达100.

3．图形的移动(翻转，平移，旋转)

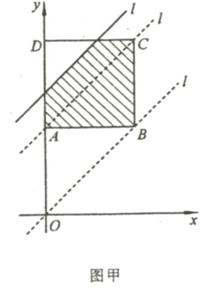
例19 (河南省2004)如图甲，边长为2的正方形ABCD中，顶点A的坐标是(0，2)．一次函数y = x + t的图像l随t的不同取值变化时，位于l的右下方由l和正方形的边围成的图像面积为S(阴影部分)

(1)　　 当t取何值时，S=3

(2)　　 在平面直角坐标系下(如图乙)，画出S与t的图像。

　4. 与一次函数有关的实际问题 　　　　　　　例20--例24

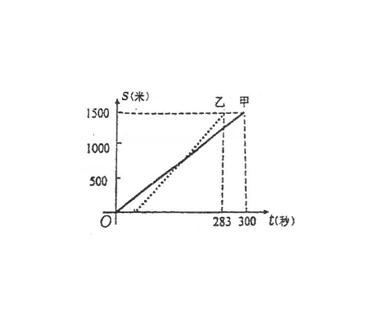
例21 甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示(实线为甲的路程与时间的关系图像，虚线为乙)，小王根据图像得到如下四个信息，其中错误的是：　　　　　 (　　 )

　　 (A) 这是一次1500米的赛跑

(B) 甲、乙两人中先到达终点的是乙

(C) 甲、乙同时起跑

(D) 甲在这次赛跑中的速度为5m/s

反比例函数

[基本题型，基本方法]

1. 反比例函数的解析式与它的图象上的点 　　例26，例27

例27 (1)(安徽省2003年) 近视眼镜的度数 y(度)与镜片焦距 x(米)成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数 y 与镜片焦距 x 之间的函数关系式是　　　　 . (优选y = )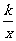

(2) 已知 y = ( 2 - m )x ^{m - 4}是反比例函数，则 m = 　　　, 此函数图象在

第　　　 象限.　　 (优选y = kx ^{- 1}　 )

(3)(北京市海淀区2003年)已知反比例函数 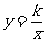　的图象经过

点(1，2)，则函数 y = - kx 可确定为(　 ).　 ( 优选k = xy )

(A)y = - 2x 　(B) y = 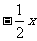　(C) 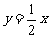　(D)y = 2x

2. 反比例函数中的数形结合(依形判数、由数思形)

看反比例函数图象： 　　　　　　　　　　　例28--例30

一看图象的位置定 k的符号：