
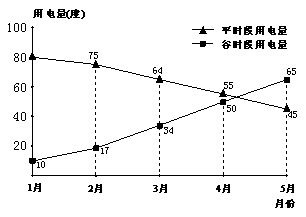
7.[05上海]小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图7),同时将前4个月的用电量和相应电费制成表格(如表1)
根据上述信息,解答下列问题:
(1)计算5月份的用电量和相应电费,将所得结果填入表1中;
(2)小明家这5个月的月平均用电量为 度;
(3)小明家这5个月的月平均用电量呈 趋势(选择“上升”或“下降”);这5个月每月电费呈 趋势(选择“上升”或“下降”);
(4)小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.
|
|
月用电量(度) |
电费(元) |
|
1月 |
90 |
51.80 |
|
2月 |
92 |
50.85 |
|
3月 |
98 |
49.24 |
|
4月 |
105 |
48.55 |
|
5月 |
|
|
[解]
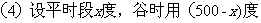
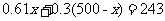

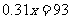
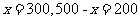
6.[05锦州]某市有A、B、C、D四个大型超市,分别位于一条东西走向的平安大路两侧,如图所示,请建立适当的直角坐标系,并写出四个超市相应的坐标.
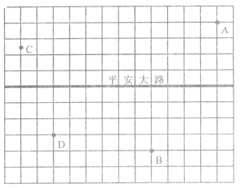
[解]评价要求:(1)直角坐标系建立正确得2分(包括原点、单位长度和正方向);
(2)A,B,C,D的坐标正确各得1分,合计6分.
5.[05南通海门]如图,在平面直角坐标系中,已知A(-10,0),B(-8,6),O为坐标原点,△OAB沿AB翻折得到△PAB.将四边形OAPB先向下平移3个单位长度,再向右平移m(m>0)个单位长度,得到四边形O1A1P1B1.设四边形O1A1P1B1与四边形OAPB重叠部分图形的周长为l.
(1)求A1、P1两点的坐标(用含m的式子表示);
(2)求周长l与m之间的函数关系式,并写出m的取值范围.
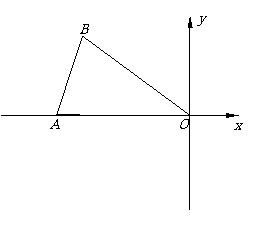
[解](1)过点B作BQ⊥OA于点Q.(如图1)
∵ 点A坐标是(-10,0),
 ∴点A1坐标为(-10+m,-3),OA=10.
∴点A1坐标为(-10+m,-3),OA=10.
又∵ 点B坐标是(-8,6),
∴BQ=6,OQ=8.
在Rt△OQB中,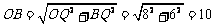 .
.
∴OA=OB=10,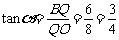 .
.
由翻折的性质可知,PA=OA=10,PB=OB=10, ∴四边形OAPB是菱形,
∴PB∥AO,∴P点坐标为(-18,6),
∴P1点坐标为(-18+m,3).
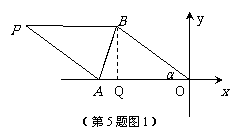
(2)①当0<m≤4时,(如图2), 过点B1作B1Q1⊥x轴于点Q1,则B1 Q1=6-3=3,
设O1B1 交x轴于点F, ∵O1B1∥BO, ∴∠α=∠β,
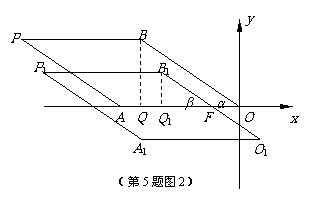 在Rt△FQ1B1中,
在Rt△FQ1B1中,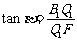 , ∴
, ∴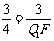 , ∴Q1F=4,
, ∴Q1F=4,
∴B1F= =5,
=5,
∵AQ=OA-OQ=10-8=2,
∴AF=AQ+QQ1+ Q1F=2+m+4=6+m,
∴周长l=2(B1F+AF)=2(5+6+m)
=2 m+22;
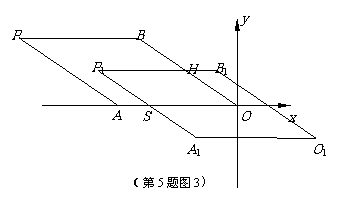 ②当4<m<14时,(如图3)
②当4<m<14时,(如图3)
设P1A1交x轴于点S,P1B1交OB
于点H,
由平移性质,得 OH=B1F=5,
此时AS=m-4,
∴OS=OA-AS=10-(m-4)=14-m,
∴周长l=2(OH+OS)=2(5+14-m)
=-2 m+38.
4.[05南通]在平面直角坐标系中,直线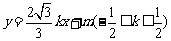 经过点A(
经过点A(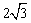 ,4),且与
,4),且与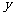 轴相交于点C.点B在
轴相交于点C.点B在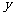 轴上,O为为坐标原点,且
轴上,O为为坐标原点,且 .记
.记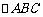 的面积为S.
的面积为S.
(1)求m的取值范围;
(2)求S关于m的函数关系式;
(3)设点B在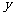 轴的正半轴上,当S取得最大值时,将
轴的正半轴上,当S取得最大值时,将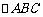 沿AC折叠得到
沿AC折叠得到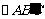 ,求点
,求点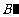 的坐标.
的坐标.
[解]⑴∵直线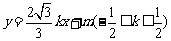 经过点A(
经过点A(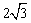 ,4),∴
,4),∴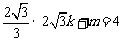 ,
,
∴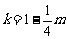 .∵
.∵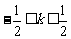 ,∴
,∴ .解得
.解得 .
.
⑵∵A的坐标是(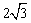 ,4),∴OA=
,4),∴OA=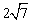 .
.
又∵ ,∴OB=7.∴B点的坐标为(0,7)或(0,-7).
,∴OB=7.∴B点的坐标为(0,7)或(0,-7).
直线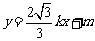 与
与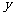 轴的交点为C(0,m).
轴的交点为C(0,m).
①
当点B的坐标是(0,7)时,由于C(0,m),  ,故BC=7- m.
,故BC=7- m.
∴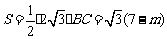 .
.
②当点B的坐标是(0,-7)时,由于C(0,m),  ,故BC=7+m.
,故BC=7+m.
∴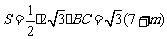 .
.
⑶当m=2时,一次函数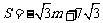 取得最大值
取得最大值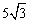 ,这时C(0,2).
,这时C(0,2).
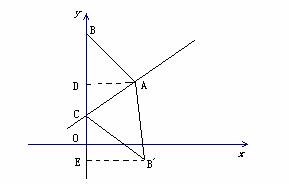
如图,分别过点A、B′作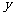 轴的垂线AD、B′E,垂足为D、E.则AD=
轴的垂线AD、B′E,垂足为D、E.则AD=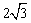 ,CD=4-2=2.在Rt
,CD=4-2=2.在Rt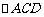 中,tan∠ACD=
中,tan∠ACD=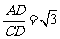 ,∴∠ACD=60°.由题意,得∠AC B′=∠ACD=60°,C B′=BC=7-2=5,∴∠B′CE=180°-∠B′CB=60°.
,∴∠ACD=60°.由题意,得∠AC B′=∠ACD=60°,C B′=BC=7-2=5,∴∠B′CE=180°-∠B′CB=60°.
在Rt 中,∠B′CE=60°,C B′=5,∴CE=
中,∠B′CE=60°,C B′=5,∴CE=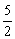 ,B′E=
,B′E=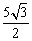 .故OE=CE-OC=
.故OE=CE-OC=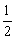 .
.
∴点B′的的坐标为(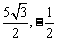 )
)
3.[05南京]某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:
根据图象解答下列问题:
(1) 洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2) 已知洗衣机的排水速度为每分钟19升,
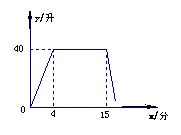 ①求排水时y与x之间的关系式。②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
①求排水时y与x之间的关系式。②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
[解](1)4分钟,40升 (2)y=-19x+325 , 2升
2.[05南京]如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,
定点M叫做对称中心。此时,M是线段PQ的中点。
 如图,在直角坐标系中,⊿ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0)。点列P1、P2、P3、…中的相邻两点都关于⊿ABO的一个顶点对称:
如图,在直角坐标系中,⊿ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0)。点列P1、P2、P3、…中的相邻两点都关于⊿ABO的一个顶点对称:
点P1与点P2关于点A对称,点P2与点P3关于点B对称,
点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5
与点P6关于点B对称,点P6与点P7关于点O对称,…。对称
中心分别是A、B,O,A,B,O,…,且这些对称中心依次循
环。已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标。
[解]P2(1,-1) P7(1,1) P100=(1,-3)
1.[05杭州]在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得ΔAOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,……,PK,(有k个就标到PK为止,不必写出画法)
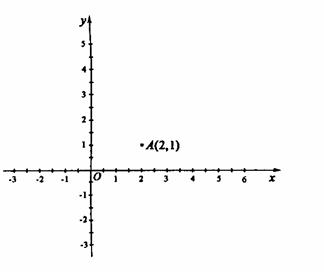
[解]  ,
, ,
, 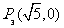 ,
,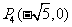 ,
,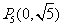 ,
, 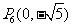 ,
,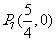 ,
,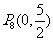
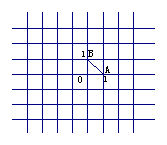
23.[05杭州]如图的围棋盘放在某个平面直角坐标系内,白棋② 的坐标为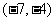 ,
,
 白棋④的坐标为
白棋④的坐标为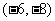 ,那么黑棋①的坐标应该是 .
,那么黑棋①的坐标应该是 .
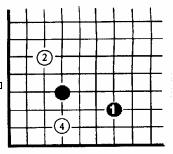

(23题图)
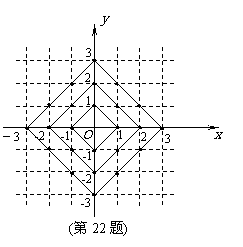
22.[05东营]在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点. 观察图
中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有____ _____个.
21.[05重庆课改]已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右
运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度.在平面直角坐标系内,现有一动点P第1次从原点O出发按甲方式运动到点P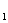 ,第2次从点P
,第2次从点P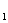 出发按乙方式运动到点P
出发按乙方式运动到点P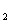 ,第3次从点P
,第3次从点P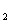 出发再按甲方式运动到点P
出发再按甲方式运动到点P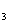 ,第4次从点P
,第4次从点P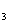 出发再按乙方式运动到点P
出发再按乙方式运动到点P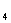 ,…….依此运动规律,则经过第11次运动后,动点P所在位置P
,…….依此运动规律,则经过第11次运动后,动点P所在位置P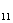 的坐标是
.
的坐标是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com