1．[05资阳]如图9，已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标

为(2,0).

(1) 求点B的坐标；

(2) 若二次函数y=ax²+bx+c的图象经过A、B、O三点，求此二次函数的解析式；

(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由.

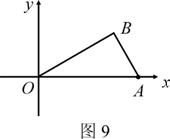
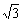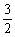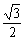[解](1) 在Rt△OAB中，∵∠AOB=30°，∴ OB=. 过点B作BD垂直于x轴，垂足为D，则　 OD=，BD=，∴ 点B的坐标为() .

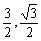(2) 将A(2,0)、B(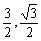)、O(0,0)三点的坐标代入y=ax²+bx+c，得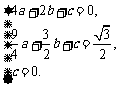

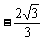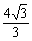解方程组，有　 a=，b=，c=0.

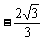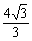∴ 所求二次函数解析式是 y=x²+x.

(3) 设存在点C(x , 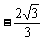x²+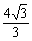x) (其中0<x<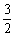)，使四边形ABCO面积最大.

∵△OAB面积为定值，

∴只要△OBC面积最大，四边形ABCO面积就最大.

过点C作x轴的垂线CE，垂足为E，交OB于点F，则

S_△OBC= S_△OCF +S_△BCF==，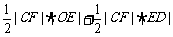

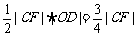而 |CF|=y_C-y_F=，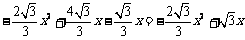

∴ S_△OBC= .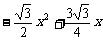

∴ 当x=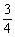时，△OBC面积最大，最大面积为.

此时，点C坐标为(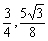)，四边形ABCO的面积为.

7.[05重庆课改]抛物线y＝+3的顶点坐标是　　　　．

6.[05东营] 已知抛物线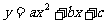经过点A(－2,7)，B(6,7)，C(3,－8)，则该抛

物线上纵坐标为－8的另一点的坐标是__________

5.[05梅州]根据图1中的抛物线，当x　　　　　 时，y随x的增大而增大，

当x　　　　 　时，y随x的增大而减小，当x　　　　　 时，y有最大值。

4.[05常德]请写出一个开口向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)　　　　　　　　　　 　。

3.[05上海]如果将二次函数的图象沿y轴向上平移1个单位，那么所得图象

的函数解析式是　　　　

2.[05枣庄]已知抛物线y=ax²+bx+c经过点A(-2，7)，B(6，7)，C(3，-8)，则该抛物线上纵坐标为-8的另一点的坐标是_________·

1.[05温州]若二次函数y＝x²－4x+c的图象与x轴没有交点，其中c为整数，则c＝_________.(只要求写出一个)抛物线的解析式　　　　　　　　　　　 。

20.[05湘潭]如图；抛物线y=ax²+bx+c(a≠0)的图像与x轴的一个交点

是(-2，0)，顶点是(1，3)。下列说法中不正确的是

A．抛物线的对称轴是x=1　　

B．抛物线的开口向下

C．抛物线与x轴的另一个交点是(2，0)

D．当x=1时，y有最大值是3

19.[05包头]已知二次函数y=x²+bx+3，当x=-1时，y取得最小值，则这个二次函数图像的顶点在(　 )

A．第一象限　 　　B．第二象限　 　　　C．第三象限　 　　D．第四象限