
11.[05常德]已知正比例函数y=kx与反比例函数y=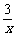 的图象都过A(m,,1)点,求此正比例函数解析式及另一个交点的坐标.
的图象都过A(m,,1)点,求此正比例函数解析式及另一个交点的坐标.
[解]∵y=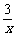 图象过A(m,1)点,则1=
图象过A(m,1)点,则1=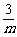 ,∴m=3,即A(3,1).将A(3,1)代入
,∴m=3,即A(3,1).将A(3,1)代入
y=kx,得k= ,∴正比例函数解析式为y=
,∴正比例函数解析式为y= x.又
x.又 x=
x=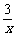 ∴x=±3.当x=3时,y=1;当x=-3时,y=-1.∴另一交点为(-3,-1).
∴x=±3.当x=3时,y=1;当x=-3时,y=-1.∴另一交点为(-3,-1).
10.[05泸州]一天上行6点钟,汪老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程S(km)(即离开学校的距离)与时间(h)的关系可用图4中的折线表示,根据图4提供的有关信息,解答下列问题:
(1)开会地点离学校多远?
(2)求出汪老师在返校途中路程S(km)与时间t(h)的函数关系式;
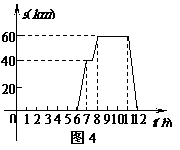 (3)请你用一段简短的话,对汪老师从上午6点到中午12点的活动情况进行描述.
(3)请你用一段简短的话,对汪老师从上午6点到中午12点的活动情况进行描述.
[解](1)开会地点离学校有60千米
(2)设汪老师在返校途中S与t的函数关系式为S=kt+b(k≠0).
由图可知,图象经过点(11,60)和点(12,0)
∴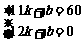 解之,得
解之,得
∴S=-60t+720(11≤t≤12)
(3)汪老师由上午6点钟从学校出发,乘车到市里开会,到了40公里处时,发生了堵车,堵了约30分钟才通车,在8占钟准里到达会场开了3个小时的会,会议一结束就返校,结果在12点钟到校.
7.[05锦州]温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(°F),设摄氏温度为x(℃),华氏温度为y(°F),则y是x的一次函数.
(1)仔细观察图中数据,试求出y与x之间的函数表达式;
(2)当摄氏温度为零下15℃时,求华氏温度为多少?

[解]
6.[05泰州] 教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
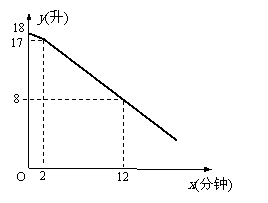
[解]设存水量y与放水时间x的解析式为y=kx+b
把(2,17)、(12,8)代入y=kx+b得
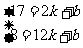 解得k=-
解得k=-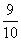 ,b=
,b=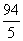
y=-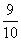 x+
x+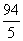 (2≤x≤
(2≤x≤ )
)
(2)由图可得每个同学接水量是0.25升 则前22个同学需接水0.25×22=5.5升
存水量y=18-5.5=12.5升 ∴12.5=-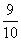 x+
x+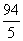 ∴x=7
∴x=7
∴前22个同学接水共需7分钟.
(3)当x=10时 存水量y=-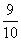 ×10+
×10+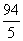 =
=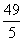
用去水18-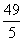 =8.2升 8.2÷0.25=32.8
=8.2升 8.2÷0.25=32.8
∴课间10分钟最多有32人及时接完水.
或 设课间10分钟最多有z人及时接完水
由题意可得 0.25z≤8.2 z≤32.8
5.[05宿迁]
在“五一黄金周”期间,小明和他的父母坐游船从甲地到乙地观光,在售票大厅看到表(一), 爸爸对小明说:“我来考考你,你能知道里程与票价之间有何关系吗?”小明点了点头说:“里程与票价是一次函数关系,具体是……”.
在游船上,他注意到表(二),思考一下,对爸爸说:“若游船在静水中的速度不变,那么我还能算出它的速度和水流速度.”爸爸说:“你真聪明!”亲爱的同学,你知道小明是如何求出的吗?请你和小明一起求出:
(1)票价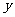 (元)与里程
(元)与里程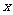 (千米)的函数关系式;
(千米)的函数关系式;
(2)游船在静水中的速度和水流速度.
|
|
里程(千米) |
票价(元) |
|
甲→乙 |
16 |
38 |
|
甲→丙 |
20 |
46 |
|
甲→丁 |
10 |
26 |
|
… |
… |
… |
|
|
出发时间 |
到达时间 |
|
甲→乙 |
8:00 |
9:00 |
|
乙→甲 |
9:20 |
10:00 |
|
甲→乙 |
10:20 |
11:20 |
|
… |
… |
… |
表(一) 表(二)
[解](1)设票价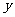 与里程
与里程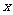 关系为
关系为 ,
,
当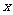 =10时,
=10时,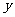 =26;当
=26;当 =20时,
=20时,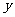 =46;
=46;
∴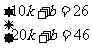 解得:
解得: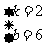 .
.
∴票价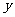 与里程
与里程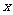 关系是
关系是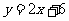 .
.
(2)设游船在静水中速度为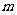 千米/小时,水流速度为
千米/小时,水流速度为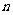 千米/小时,
千米/小时,
根据图中提供信息,得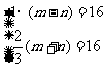 , 解得:
, 解得: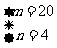 .
.
答:游船在静水速度为20千米/小时,水流速度为4千米/小时.
4.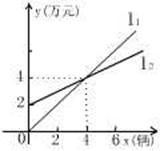 [05十堰课改]如图,
[05十堰课改]如图,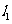 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系;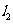 表示摩托车厂一天的销售成本与销售量的关系。
表示摩托车厂一天的销售成本与销售量的关系。
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入-成本)
[解](1)y=x
(2)设 ∵直线过(0,2)、(4,4)两点
∵直线过(0,2)、(4,4)两点
∴ 又
又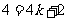 ∴
∴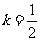 ∴
∴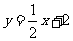
(3)由图像知,当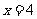 时,销售收入等于销售成本
时,销售收入等于销售成本
或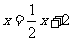 ∴
∴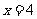
(4)由图像知:当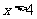 时,工厂才能获利
时,工厂才能获利
或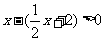 时,即
时,即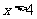 时,才能获利。
时,才能获利。
3.[05温州]如图,在平面直角坐标系中,正方形AOCB的边长为6,O为坐标原点,边
OC在x轴的正半轴上,边OA在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE∶S四边形AOCE=1∶3。

⑴ 求出点E的坐标; ⑵ 求直线EC的函数解析式.
[解]⑴ ∵S△FAE∶S四边形AOCE=1∶3, ∴S△FAE∶S△FOC=1∶4,
∵四边形AOCB是正方形, ∴AB∥OC, ∴△FAE∽△FOC,
∴AE∶OC=1∶2,
∵OA=OC=6, ∴AE=3, ∴点E的坐标是(3,6)
⑵ 设直线EC的解析式是y=kx+b,
∵直线y=kx+b过E(3,6)和C(6,0)
∴,解得:
∴直线EC的解析式是y=-2x+12
4.[05遂宁课改]某商场的营业员小李销售某种商品,他的月收入与他该月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
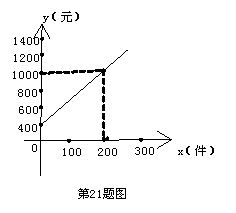
(1)求出小李的个人月收入y(元)与他的月销售量x(件)(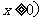 之间的函数关系式;
之间的函数关系式;
(2)已知小李4月份的销售量为250件,求小李4月份的收入是多少元?
[解](1)由题意可设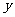 与
与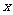 的函数关系式为:
的函数关系式为: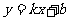
由图象可知:当 时,
时,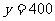 ,
,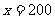 时,
时,
有
解得,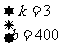
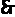
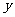 与
与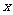 的函数关系式为:
的函数关系式为: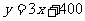
(2)当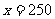 时,
时,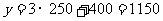 (元)
(元)
答:小李4月份的收入为 元。
元。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com