
9. B 10.C 11.D 12.D 13.D 14.D 15.A 16. A
1.B 2. A 3.D 4.D 5. A 6.D 7.C 8.C
3.[05黄石]一次函数y=x+b与反比例函数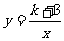 图像的交点为A(m,n),且m,n(m<n)
图像的交点为A(m,n),且m,n(m<n)
是关于x的一元二次方程kx2+(2k-7)x+k+3的两个不相等的实数根,其中k为非负整数,m,n为常数。
(1)求k的值;
(2)求A的坐标与一次函数解析式。
[解](1)由方程有两个不相等的实数根,得:
△= =
= ∴
∴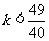
又∵k为非负整数 ∴k=0,1
当k=0时,方程kx2+(2k-7)x+k+3=0不是一元二次方程,与题设矛盾
∴k=1
(2)当k=1时,方程x2-5x+4=0 ∴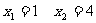
∵m<n ∴m=1 n=4 即A点的坐标为(1,4)
把A(1,4)坐标代入y=x+b得b=3
∴所求函数解析式为y=x+3
选择题、填空题答案
2.[05厦门]已知:O是坐标原点,P(m,n)(m>0)是函数y = (k>0)上的点,
过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m). 设△OPA的面积为s,且s=1+.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3 ) 设n是小于20的整数,且k≠,求OP2的最小值.
[解]过点P作PQ⊥x轴于Q,则PQ=n,OQ=m
(1)当n=1时, s= ∴ a==
(2)解1: ∵ OP=AP PA⊥OP ∴△OPA是等腰直角三角形
∴ m=n= ∴ 1+=·an
即n4-4n2+4=0
∴ k2-4k+4=0
∴ k=2
解2:∵ OP=AP PA⊥OP ∴△OPA是等腰直角三角形 ∴ m=n
设△OPQ的面积为s1 则:s1= ∴ ·mn=(1+)
即:n4-4n2+4=0 ∴ k2-4k+4=0
∴ k=2
(3)解1:∵ PA⊥OP, PQ⊥OA ∴ △OPQ∽△OAP
设:△OPQ的面积为s1,则=
即: =
化简得:2n4+2k2-k n4-4k=0 (k-2)(2k-n4)=0
∴k=2或k=(舍去) ∴当n是小于20的整数时,k=2.
∵ OP2=n2+m2=n2+
又m>0,k=2, ∴ n是大于0且小于20的整数
当n=1时,OP2=5
当n=2时,OP2=5
当n=3时,OP2=32+=9+=
当n是大于3且小于20的整数时,
即当n=4、5、6、…、19时,OP2得值分别是:
42+、52+、62+、…、192+
∵192+>182+>…>32+>5
∴ OP2的最小值是5.
解2: ∵ OP2=n2+m2=n2+=n2+=(n-)+4
当n= 时,即当n=时,OP2最小;
又∵n是整数,而当n=1时,OP2=5;n=2时,OP2=5
∴ OP2的最小值是5.
解3:∵ PA⊥OP, PQ⊥OA ∴ △OPQ∽△P AQ
= =
化简得:2n4+2k2-k n4-4k=0 (k-2)(2k-n4)=0
∴k=2或k=(舍去)
解4:∵ PA⊥OP, PQ⊥OA ∴ △OPQ∽△P AQ
= 化简得:2n4+2k2-k n4-4k=0 (k-2)(2k-n4)=0
∴k=2或k=(舍去)
解5:∵ PA⊥OP, PQ⊥OA ∴ △OPQ∽△OAP ∴ = ∴ OP2=OQ·OA
化简得:2n4+2k2-k n4-4k=0 (k-2)(2k-n4)=0
∴k=2或k=(舍去)
1.[05临沂课改]某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
|
年 度 |
2001 |
2002 |
2003 |
2004 |
|
投入技改资金z(万元) |
2.5 |
3 |
4 |
4.5 |
|
产品成本(万元/件) |
7.2 |
6 |
4.5 |
4 |
(1)请你认真分析表中数据,从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
(2)按照这种变化规律,若2005年已投人技改资金5万元.
① 预计生产成本每件比2004年降低多少万元?
② 如果打算在2005年把每件产品成本降低到3.2万元,则还需投入技改资金多少万元(结果精确到0.01万元)?
[解](1)设其为一次函数,解析式为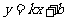
当 时,
时,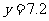 ; 当
; 当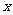 =3时,
=3时,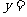 6.
6.
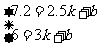 解得
解得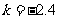 ,
,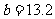 ∴一次函数解析式为
∴一次函数解析式为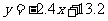
把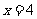 时,
时,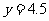 代人此函数解析式,左边≠右边. ∴其不是一次函数.
代人此函数解析式,左边≠右边. ∴其不是一次函数.
同理.其也不是二次函数.
设其为反比例函数.解析式为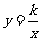 。 当
。 当 时,
时,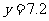 ,
,
可得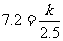 解得
解得 ∴反比例函数是
∴反比例函数是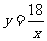 。
。
验证:当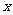 =3时,
=3时,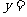
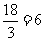 ,符合反比例函数。
,符合反比例函数。
同理可验证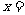 4时,
4时,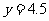 ,
,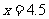 时,
时,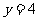 成立。
成立。
可用反比例函数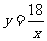 表示其变化规律。
表示其变化规律。
(2)解:①当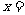 5万元时,,
5万元时,,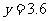 。
。 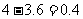 (万元),
(万元),
∴生产成本每件比2004年降低0.4万元。
②当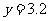 时,
时,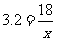 。 ∴
。 ∴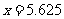
∴
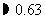 (万元)
(万元)
∴还约需投入0.63万元.
14.[05黄岗]反比例函数y = 的图象经过点(tan45°,cos60°),则k = ;
13.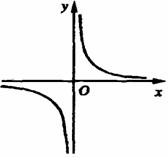 [05毕节]反比例函数y=
[05毕节]反比例函数y= (m为常数)的图像如图所示,则m的取值范围是________________________。
(m为常数)的图像如图所示,则m的取值范围是________________________。
12.[05漳州]请你写出一个点坐标,使这点在反比例函数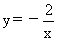 的图象上,则这个点的坐标为 。
的图象上,则这个点的坐标为 。
11.[05锦州]在某数学小组的活动中,组长为大家出了一道函数题:这是一个反比例函数,并且y随x的增大而减小.请你写山一个符合条件的函数表达式________________.
10.[05南通]如图,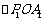 、
、 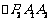 是等腰直角三角形,点
是等腰直角三角形,点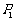 、
、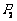 在函数
在函数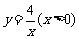 的图象上,斜边
的图象上,斜边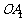 、
、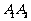 都在
都在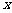 轴上,则点
轴上,则点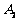 的坐标是________________.
的坐标是________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com