25．(本题满分l2分)

如图，四边形OABC为直角梯形，A(4，0)，B(3，4)，C(0，4)．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动，其中一个动点到达终点时，另一个动点也随之停止运动。过点N作NP垂直轴于点P，连结AC交NP于Q，连结MQ．

(1)点____________(填M或N)能到达终点；

(2)求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，当t为何值时，S的值最大；

(3)是否存在点M，使得△AQM为直角三角形?若存在，求出点M的坐标，若不存在，说明理由．

2008年聊城市高唐初三学业水平诊断性评价

24．(本题满分l0分)

某污水处理公司为学校建一座三级污水处理池，平面图形为矩形，面积为200平方米(平面图如图所示的ABCD)．已知池的外围墙建造单价为每米400元．中间两条隔墙建造单价每米300元，池底建造的单价为每平方米80元(池墙的厚度不考虑)

(1)如果矩形水池恰好被隔墙分成三个正方形，试计算此项工程的总造价(精确到100元)

(2)如果改变矩形水池的形状(面积不变)，问预算45600元总造价，能否完成此项工程?试通过计算说明理由

(3)请估算此项工程的最低造价(多出部分只要不超过100元就有效)

23．(本题满分8分)

为发展电信事业，方便用户，电信公司对移动电话采取不同的收费方式，其中，所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间(min)与通话费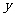(元)的关系如图所示：

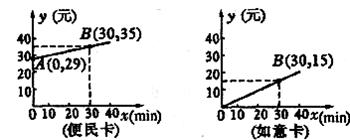
(1)分别求出通话费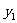、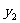与通话时间之间的函数关系式；

(2)请帮用户计算，在一个月内使用哪一种卡便宜?

22．(本题满分8分)

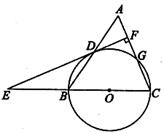
如图，等腰三角形ABC中，AC=BC=10，AB=12．以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．

(1)求证：直线EF是⊙O的切线；

(2)求sin∠E的值．

21．(本题满分8分)

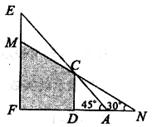
如图，CD，EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，求AN之间的距离．

19．(本题满分8分)

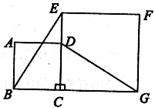
如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG．

求证：BE=DG

18．(本题满分7分)

　　 先化简，再求值：(3+2)(3一2)一5(一l)一(2一l)²，其中=－

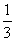
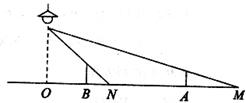
17．如图，路灯距地面8米，身高1.6米的小明从距离路灯的底部(点O)20米的点A处，沿OA所在的直线行走14米到点B时，则人影的长度____________(填增加或减少多少)

16．观察下列各式：(一l)(+1)=²一l；(一l)(²++1)=³-1；(一l)(³+²++1)　 =⁴-1；……………………；

根据前面各式的规律可得到(一l)(ⁿ+^n-1+^n-2+…++1)=_____________．