16.70°　 17.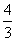　 18.一次函数的解析式为：y=2x+1；反比例函数的解析式为： 19.15°或75°

11.二、四　　 12.5　 13.y=；x= 1；(1，-1)　 14. 5， 　15.

1.B　　 2.D　 3.C　　 4.A　　 5.D　　 6.C　　 7.B　　 8.D　　 9. B　　 10.A

27. (本小题9分)如图，在直角坐标系xoy中，点A(2，0)，点B在第一象限且△OAB为等边三角形，

△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．

(1)判断点C是否为弧OB的中点？并说明理由；

(2)求B、C两点的坐标；

(3)求直线CD的函数解析式；

(4)点P在线段OB上，且满足四边形OPCD是等腰梯形，求点P坐标.

北京市房山区2008-2009学年度第一学期期末试题答案及评分标准

九年级数学

26.(本小题10分)如图,　　　 抛物线与x轴的一个交点是A，与y轴的交点是B，且OA、OB(OA＜OB)的长是方程的两个实数根.

(1)求A、B两点的坐标；

　(2) 求出此抛物线的的解析式及顶点D的坐标；

(3)求出此抛物线与x轴的另一个交点C的坐标;

(4)在直线BC上是否存在一点P，使四边形PDCO为梯形？若存在，求出P点坐标，若不存在，说明理由.

25. (本小题8分)如图，AB为⊙O的直径，割线PCD交⊙O于C、D, .

(1)求证：PA是⊙O的切线；

(2)若PA=6，CD=3PC，求PD的长.

24. (本小题6分) 如图，OA、OC是⊙O的半径，OA＝1，且OC⊥OA，点D在弧AC上，弧AD＝2弧CD,在OC求一点P,使PA+PD最小，并求这个最小值.

23. (本小题6分) 如图，在梯形中，，，，，，求的长．

22. (本小题8分)有3张背面相同的纸牌A，B，C，其正面分别画有三个不同的图形(如图)将这3张纸牌背面朝上洗匀后摸出1张，放回洗匀后再摸1张.

(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A，B，C表示)；

(2)求摸出两张牌面图形都是轴对称图形的纸牌的概率；

　(3)小华和小明玩游戏，规定：若摸出两张牌面图形都是轴对称图形的纸牌，则小华赢；否则，小明赢.请你说明此规定是否公平.

21. (本小题7分)已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于D，BC=4cm．

(1)求证：AC⊥OD；

(2)求OD的长；　　　　　　　　　

(3)若2sinA－1=0，求⊙O的直径．