
21.(本题满分12分)
解法一:在Rt△BCE中,EC=20,∠C=90°,∠BEC=60°
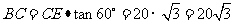 (米)。。。。。。。。。。6分(表达式2分+4分)
(米)。。。。。。。。。。6分(表达式2分+4分)
在Rt△BCF中,∠C=90°,∠F=30°
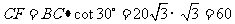 。。。。。12分(表达式2分+4分)
。。。。。12分(表达式2分+4分)
答:略(不答扣1分)
 解法二:在Rt△BCE中,EC=20,∠C=90°,∠BEC=60°
解法二:在Rt△BCE中,EC=20,∠C=90°,∠BEC=60°
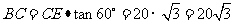 (米)。。。。。。。。。6分
(米)。。。。。。。。。6分
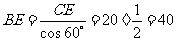 。。。。。。。。。。。。8分
。。。。。。。。。。。。8分
∵∠C=90°,∠BEC=60°,∠BEC=30°
∴∠FBE=∠BEC-∠F =60°-30°=30°。。。。。。。。。。。。10分
∴EF=EB=40。。。。。。。。。。。。11分
∴CF =60(米)。。。。。。。。。。。。。。。12分
注:如有其它解法结果正确,有相应的正确解答过程,也给满分。
20.(本题满分10分)
 |
1 |
2 |
|
3 |
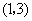 |
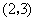 |
|
4 |
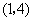 |
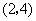 |
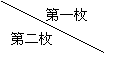
(1)列表法: 。。。。。。。。。。。。。。。。。。。。。。 4分
 |
1 |
2 |
|
3 |
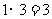 |
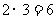 |
|
4 |
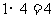 |
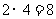 |
从表中可看出:事件发生的所有可能的结果总数为4,积为奇数的结果总数为2,。。。。5分
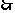 积为奇数的概率
积为奇数的概率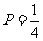 。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。6分
(2)如表(可以不用表)
因为有四点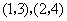 在函数
在函数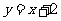 的图象上, 。。。。。。。。。。。。。。。。。。。。。。8分
的图象上, 。。。。。。。。。。。。。。。。。。。。。。8分
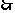 所求概率为
所求概率为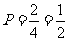 。。。。。。。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。。。。。。。10分
注: 表格中间的结果部分写成“ 1,3”有逗号给满分,写成“13”没逗号就扣4分
19.(本题满分10分)
解:设走道的宽度为x m,。。。。。。。。。。。。。。。。。。。。。。。1分
依题意列方程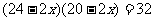 .。。。。。。。。。。。。。。。。。。。。。。。4分
.。。。。。。。。。。。。。。。。。。。。。。。4分
化简 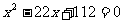 .。。。。。。。。。。。。。。。。。。。。6分
.。。。。。。。。。。。。。。。。。。。。6分
解得  ,
, 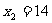 . 。。。。。。。。。。。。。。。。。。。。。。 8分
. 。。。。。。。。。。。。。。。。。。。。。。 8分
但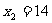 不合题意,符合本题要求的解是
不合题意,符合本题要求的解是 (m). 。。。。。。。。。。10分
(m). 。。。。。。。。。。10分
注:在14 旁注明了(舍去)或有此意思就给2分
如果解方程出错,如解得8,和-14,舍去了-14,只扣解方程的2分
两个解都错,就扣4分
答:略。。。。。。。。。。。。。。。。。。。。。。。不答扣1分
18.(本题满分9分)
已知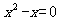 ,试求式子
,试求式子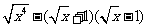 的值.
的值.
解法一:由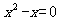 得:
得: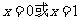 。。。。。。。。。。。。。。。。。。。。。。。3分(2分+1分)
。。。。。。。。。。。。。。。。。。。。。。。3分(2分+1分)
.注:只写1个给2分,写对两个给3分
当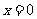 ,
,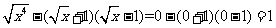 。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。6分
当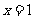 ,
,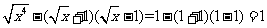 。。。。。。。。。。。。。。。。9分
。。。。。。。。。。。。。。。。9分
注:代入正确给2分
解法一: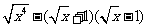
=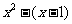 。。。。。。。。。。。。。。。。。。。。。。。5分(2分+3分)
。。。。。。。。。。。。。。。。。。。。。。。5分(2分+3分)
注:写成x2–x–1,3分里只给1分,共给3分
=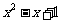 。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。7分
由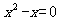 得原式=0+1=1。。。。。。。。。。。。。。。。。。。。。。。9分
得原式=0+1=1。。。。。。。。。。。。。。。。。。。。。。。9分
17.(本题满分9分)
解: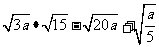
=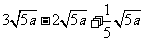 。。。。。。。。。。。。。。。。。。。。。。。7分(3分+2分+2分)
。。。。。。。。。。。。。。。。。。。。。。。7分(3分+2分+2分)
=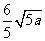 。。。。。。。。。。。。。。。。。。。。。。。9分
。。。。。。。。。。。。。。。。。。。。。。。9分
.注:只写结果无过程只给2分。
注:第12题写成“1或-1, ,
, 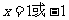 ”不扣分,只写对其中一个给1分。
”不扣分,只写对其中一个给1分。
第15题写成“2.67”等近似值的给1分。
第16题写成“0.4或40%”都不扣分。
25.(本题满分12分)
以Rt△OAB的两直角边所在的直线为轴,以直角顶点O为原点,建立直角坐标系. 如图9所示,且点A、B的坐标分别为(0,8)和(6,0).若保持线段AB的长度不变,点A在y轴正半轴上向下滑动,则点B在x轴正半轴上向右滑动.
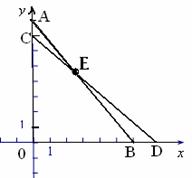 (1)求Rt△OAB斜边AB上的高h的长度.
(1)求Rt△OAB斜边AB上的高h的长度.
(2)如果点A下滑1个单位长度到点C,则点B向右滑动
到点D,猜一猜点B滑动的距离比1大,还是比1小,
或者等于1?设BD=x, 列出点B滑动距离x满足的方程,
并尝试得出这个方程的近似解.(保留一位小数)
|
天河区2007学年上学期期末考试
九年级数学评分标准
24. (本题满分14分)
(本题满分14分)
在单位长度为1的正方形网格中建立直角坐标系,如图8所示.已知点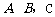 的坐标分别为(0,0),(4,0),(5,2).
的坐标分别为(0,0),(4,0),(5,2).
(1)利用位似方法,画出与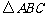 相似的
相似的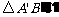
(要求位似中心在三角形的外部,相似比任定,
但图形不超过所给的方格);
(2)求出所画的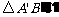 三个顶点的坐标并求出
三个顶点的坐标并求出
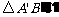 的周长.
的周长.
23.(本题满分14分)
一只箱子里放有一定数量的球,它们除颜色外均相同.
(1) 若箱子里只有2个白球与1个红球,从箱子中任意摸出一个球,不将它放回箱子,再摸出一个球,求两次摸出球的都是白球的概率,并画树状图表示.
(2)若要设计一个满足条件“摸到白球和红球的概率分别为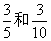 ”的游戏. 则箱子里至少需要放多少个球?请说明你的理由.
”的游戏. 则箱子里至少需要放多少个球?请说明你的理由.
22.(本题满分12分)
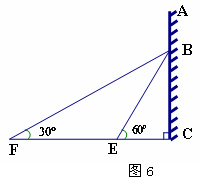
如图7,在矩形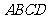 中,
中,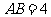 ,
,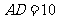 .直角尺的直角顶点
.直角尺的直角顶点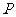 在
在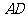 上滑动时(点
上滑动时(点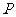 与
与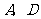 不重合),一直角边经过点
不重合),一直角边经过点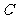 ,另一直角边
,另一直角边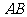 交于点
交于点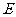 .是否存在这样的点
.是否存在这样的点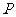 ,使
,使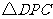 的周长等于
的周长等于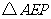 周长的
周长的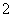 倍?若存在,求出
倍?若存在,求出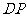 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com