
6、下列事件中是必然事件的是( )。
(A)太阳每天都从东方升起 ; (B)度量三角形的内角和结果是360°;
(C)投掷一枚硬币,正面向上; (D)某射击运动员射击一次,中靶心。
5、扇形的半径为30cm,圆心角为120°,此扇形的弧长是( )
(A)10 cm (B)20 cm (C)10πcm (D)20πcm
4、“从布袋中取出一个红球的概率为0”,这句话的含义是( )
(A) 布袋中红球很少 (B) 布袋中全是红球
(C) 布袋中没有红球 (D) 不能确定
3、 有一人患了流感,每轮传染中平均一个人传染了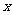 个人,则经过两轮传染后,患流感的总人数400,所列方程是 (
)
个人,则经过两轮传染后,患流感的总人数400,所列方程是 (
)
(A) =400 (B)
=400 (B)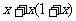 =400
=400
(C) =400 (D)
=400 (D) =400
=400
2、 下列根式中,最简二次根式是( )
A. B. C. D.
1、 式子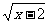 在实数范围内有意义,则X的取值范围是( )
在实数范围内有意义,则X的取值范围是( )
(A)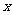 ≥
≥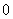 (B)
(B)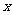
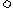
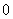 (C)
(C)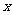 ≤2
(D)
≤2
(D)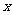 ≥2
≥2
25.(本小题满分12分)
解:(1)在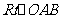 中OA=8,OB=6,则AB=10
中OA=8,OB=6,则AB=10
∵10h=6×8
∴h=4.8。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
(2)点B滑动的距离比1大。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分
设滑动距离均为x,在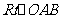 中,OC=7,OD=OB+BD=6+x
中,OC=7,OD=OB+BD=6+x
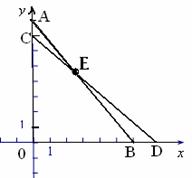
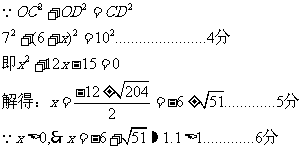
注:没有求出近似解扣1分
(3)存在。。。。。。。。。。。。。。。。。。。。。。。7分
设滑动距离均为x,

。。。。。。。。。。。。。。。。。。。。。。。8分
点A、B的坐标分别为(0,8)和(6,0)可得直线AB的解析式为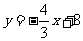
点C、D的坐标分别为(0,6)和(8,0)可得直线CD的解析式为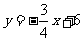
。。。。。。。。。。。。。。。。。。。。。。。10分
解方程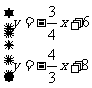 得
得 。。。。。。。。。。。。。。。。。。。。。。。11分
。。。。。。。。。。。。。。。。。。。。。。。11分
所以公共部分面积为:
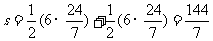 。。。。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。。。。12分
24.(本题满分14分)
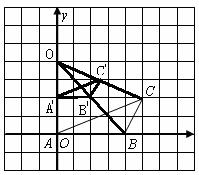
(1)如图所示,…………………………………………………………6分(只要画对)
 |
 |
||||
|
(2)如图1所示,点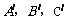 的坐标分别为(0,2),(2,0),(2.5,3)
的坐标分别为(0,2),(2,0),(2.5,3)
。。。。。。。。。。。。。。。9分(写出一个1分,结合图判断)
∵点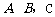 的坐标分别为(0,0),(4,0),(5,2)
的坐标分别为(0,0),(4,0),(5,2)
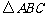 与
与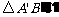 相似比为2∶1,位似中心点O坐标为(0,4)
相似比为2∶1,位似中心点O坐标为(0,4)
∴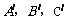 分别是OA,OB,OC的中点
分别是OA,OB,OC的中点
∴
点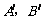 的坐标分别为(0,2),(2,0)。。。。。。。。。。。。。。。。。。。。。。。。10分
的坐标分别为(0,2),(2,0)。。。。。。。。。。。。。。。。。。。。。。。。10分
点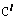 到y轴的距离为
到y轴的距离为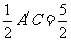
点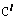 到x轴的距离为
到x轴的距离为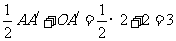
点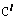 的坐标为(2.5,3)。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
的坐标为(2.5,3)。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
又AB=4,BC=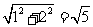 ,AC=
,AC=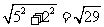
∴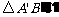 周长=
周长=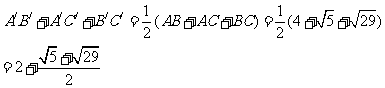
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14分
(注意:只写出坐标而没有简要过程扣3分,可利用相似、中位线、勾股定理等等,只要明白即可)
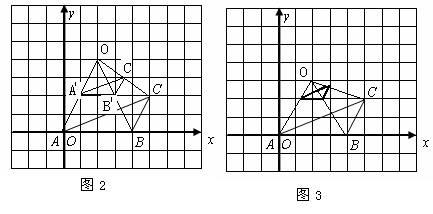
如图2所示,点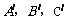 的坐标分别为(1,2),(3,2),(3.5,3)
的坐标分别为(1,2),(3,2),(3.5,3)
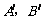 的坐标求法(略)
的坐标求法(略)
∵点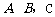 的坐标分别为(0,0),(4,0),(5,2)。对称中心O的坐标(2,0)
的坐标分别为(0,0),(4,0),(5,2)。对称中心O的坐标(2,0)
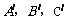 分别是OA,OB,OC的中点
分别是OA,OB,OC的中点
∴点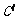 到y轴的距离为
到y轴的距离为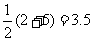 (梯形中位线)
(梯形中位线)
点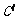 到x轴的距离为
到x轴的距离为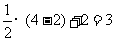
∴点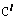 的坐标为(3.5,3)
的坐标为(3.5,3)
23.(本小题满分14分)
解:(1)记两个白球分别为白1与白2,画树状图如右所示:。。。。。。。。。。。。。4分
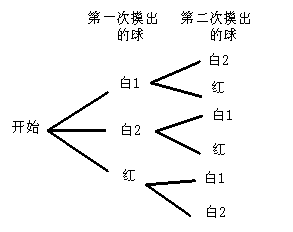
从树状图可看出:事件发生的所有可能的结果总数为6,
两次摸出球的都是白球的结果总数为2,。。。。。。。。。。。。。。。。。6分
因此其概率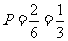 .。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
(2)箱子里至少需要放10个球。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
理由:摸到白球、红球的概率分别为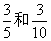 ,
,
白球与红球的数量比例为2∶1
设白球2x个,红球x个,其他颜色求y个,则箱子里需要放(3x+y)个球。。。。。。。。。。。11分
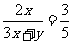 , 。。。。。。。。。。。12分
, 。。。。。。。。。。。12分
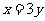 。。。。。。。。。。。。。。。。。。。。。。。。。。。13分
。。。。。。。。。。。。。。。。。。。。。。。。。。。13分
当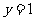 时箱子里球最少,此时白球6个,红球3个,箱子里共放10个球。
时箱子里球最少,此时白球6个,红球3个,箱子里共放10个球。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14分
22.(本小题满分12分)
 解:存在.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
解:存在.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
在矩形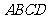 中,∠A=∠D=∠EPC=90°
中,∠A=∠D=∠EPC=90°
∠AEP+∠APE=90°
∠DPC+∠AP E=90°
∠AEP=∠DPC
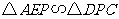 。。。。。。。。。。。。。。。。。。。。。。。。.。。。4分
。。。。。。。。。。。。。。。。。。。。。。。。.。。。4分
假设存在满足条件的点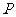 ,设
,设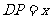 ,则
,则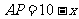
由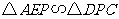 知
知 ,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
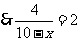 ,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
解得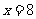 ,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com