
1.将方程 3x(x-1)= 5(x + 2)化为一元二次方程的一般式,正确的是( ).
A.4x2-4x + 5 = 0 B.3x2-8x-10 = 0
C.4x2 + 4x-5 = 0 D.3x2 + 8x + 10 = 0
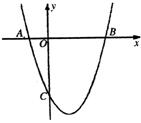
22.(本题13)如图,抛物线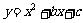 与x轴交于A(-1,0)、B(3,0)两点。
与x轴交于A(-1,0)、B(3,0)两点。
(1)求该抛物线的解析式;(3分)
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;(5分)
(3)设(1)中的抛物线交y轴于C点。在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小,若存在,求出Q点的坐标;若不存在,请说明理由。(5分)
23.(本题12分) 如图:AB是⊙O的直径,AC是⊙O上一条弦,AC在AB下方,在⊙O上存在一点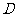 。
。
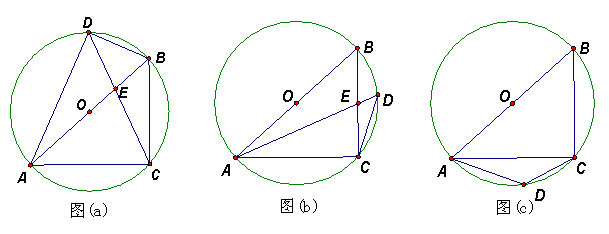
(1)(如图(a)),当D点在O点在正上方,连结AD、CD、BC、BD,CD交AB于E,则,在图中你可以发现多少对相似三角形?请列举出来,并说明理由。(4分)
(2)①(如图(b)),当D点在劣弧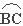 上运动(不与B、C重合)则AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;(3分)
上运动(不与B、C重合)则AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;(3分)
②(如图(c)),当D点在劣弧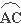 上运动(不与A、C重合)则AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;(3分)
上运动(不与A、C重合)则AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;(3分)
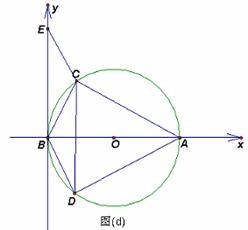
(3)如图(d), 以B点为原点,AB所在的直线为x轴,建立平面直角坐标系,∠DCA=∠CBA=60°,连结BD,过C点作CE∥DB,求证:四边形CDBE为平行四边形;(2分)
21. (本题9分)
数学是一门艺术与美妙结合的一门学科,现在做一次探究:
观察下图的图形,这是通过等边三角形绘制的一幅自相似图形。

若第1个图形中的阴影部分的面积为1。
[提出问题]经过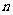 次变换,求第n个图形的阴影部分的面积。
次变换,求第n个图形的阴影部分的面积。
[解决问题](1)填写下列表格:(每空2分,共6分)
|
|
第1次 |
第2次 |
第3次 |
…… |
第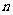 次 次 |
 |
 |
 |
 |
…… |
|
|
1 |
|
|
|
…… |
|
(2)根据你的判断,经过第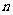 次变换后,则第n个图形的阴影部分的面积
次变换后,则第n个图形的阴影部分的面积
是 。(3分)
。
20.(本题10分)某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为60000元.
(1).一年中这个村修建了多少公顷蔬菜大棚?(5分)
(2).若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.(5分)
18.(本题9分)
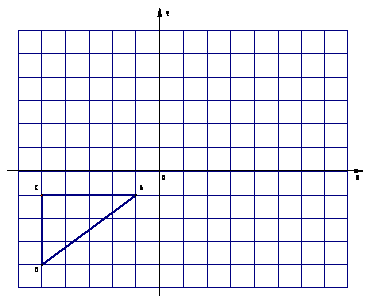
如图,已知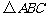 的顶点
的顶点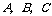 的坐标分别是A(-1,-1)B(-5,-4)C(-5,-1).
的坐标分别是A(-1,-1)B(-5,-4)C(-5,-1).
(1)、作出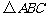 关于点P(0,-2)中心对称的图形
关于点P(0,-2)中心对称的图形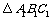 ,
,
并直接写出顶点A1、B1、C1的坐标.(3分)
(2)、将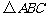 绕原点O按顺时针方向旋转90°后得到△A2B2C2,
绕原点O按顺时针方向旋转90°后得到△A2B2C2,
画出△A2B2C2,并直接写出顶点A2、B2、C2的坐标.(3分)
(3)、将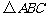 沿线段BA方向平移10个单位后得到△A3B3C3,
沿线段BA方向平移10个单位后得到△A3B3C3,
并直接写出顶点A3、B3、C3的坐标.(3分)
17、计算(本题8分):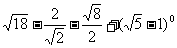
16、解方程:(每小题 8分,共16分)
(1).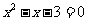 (2).
(2).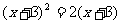
15、已知关于的函数同时满足下列三个条件
①函数的图像不经过第二象限;
②当时x﹤2时,对应的函数值y﹤0;
③当x﹤2时,函数值y随x的增大而增大。
你认为符合要求的函数的解析式可以是:____________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com