2、　 与点和圆、直线和圆的位置关系相类似，两圆的位置关系(形的关系)与两圆的半径、圆心距的大小(数量关系)有关。

(1)两圆外离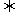d＞R+r

(2)两圆外切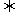d＝R+r

(3)两圆相交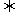R－r＜d＜R+r(R≥r)

(4)两圆内切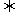d＝R－r(R＞r)

(5)两圆内含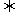d＜R－r(R＞r)

这个结论是双向的，“ ”是由两圆位置的关系，得到两圆半径与圆心距之间特定的数量关系，这是两圆位置关系的性质，利用这些性质可以把形的问题转化为数的问题来解决；“ ”是根据两圆半径与圆心距之间的某种数量关系来判定两圆的位置关系，从而把判定形的问题，转向为数的问题来解决。这在解决两圆的位置关系的问题时特别方便。

应当注意的是，判定两圆相交时，必须具备R－r＜d＜R+r的条件。这是因为只有当d＞R－r时，两圆可能相交、外切或外离；而当d＜R+r时，两圆可能相交、内切或内含。因此，只有当R－r＜d＜R+r时才能判定两圆相交。

1、　 圆和圆的位置关系的分类，既考虑了数(两圆公共点的个数)，又考虑了形(两圆的相对位置)，两圆的五种位置关系按公共点的个数(0，1，2)可分为三类：

(1)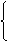没有公共点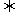相离　 外离

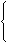　　　　　　　　　　　 　内含(包括同心)；

(2)有1个公共点相切 外切

　　　　　　　　　　　 　内切；

(3)有2个公共点相交

　　 本单元主要研究圆和圆的位置关系，内容主要包括两个圆各种不同位置关系的概念；相交、相切两圆的性质以及两个圆的公切线。其中两个圆不同位置关系的概念及相交、相切时的性质是本单元的重点。

　　 同学们在学习过程中要注意与前面所学的圆的有关知识的联系。当一条直线 与两个圆相切时，这条直线就是这两个圆的公切线，而对于每一个圆来说，这条直线都是他们的切线。因此，研究两圆的公切线问题，就是圆的切线的判定和性质在两个相关的圆中的应用。由圆的轴对称性可以推出，任意两个圆组成的图形，一定是以连心线为轴的对称图形。两圆相交、相切的性质，都是由这个对称性得到的。所以在学习这一单元时，要随时复习巩固前面所学知识，并逐步学会运用这些知识来解决两圆位置关系中的新问题。

　　 本单元学习过程中，涉及实际应用的问题较多，有计算题，也有作图题，要学会把实际问题抽象成数学问题，在关于两圆公切线长的计算中，要学会把它转化为解直角三角形的问题。

(三)证明题

1.略

2.证ED是直径,∵AD平分∠BAC,∴BD=CD 结论成立.

3.连MB,证∠BMC=∠DMB.

(二)选择填空

　 1.C　 2.C　 3.D　 4.B　 5.C

(一)填空题

　 1.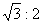　 2.60°,40°　 3.120°,60°或120°　 4.125°　 5.30°

　 6.10°　 7.55°　 8.105°　 9.5　 10.100°, 40°, 40°　 11.　

　 12.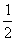　 13.15°

(二)选择填空

1.已知:点O是ΔABC的外心,∠A=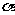,则∠BOC等于:

A.2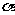　 B.360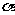°-2　　 C.2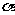或360°-2　　 D.180°-2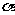

2.在⊙O中,AB=2CD,则AB与CD的关系是:

A.AB=2CD　　 B.AB>2CD　　 C.CD<AB<2CD　　 D.不确定

3.在ΔAOB中,∠O=90°,以OB为半径的⊙O分别交AB,AO与C,D.∠A=28°,则CD的度数是:

　 A.28°　　 B.56°　　 C.62°　　 D.34°

4.ΔABC内接于⊙O,OD⊥BC于D,∠BOD=38°,则∠A等于:

　 A.19°　　 B.38°或142°　　 C.19°或161°　　 D.38°

5.在⊙O中,两条直径AB⊥CD于O,弦AP交CD于Q,则AP·AQ等于:

A.AO·OB　　 B.CQ·QD　　 C.AO·AB　　 D.OQ·BP

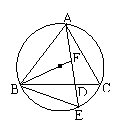(三)证明题

1.ΔABC中,∠A的平分线交BC于D.交

ΔABC外接圆于E.∠ABC的平分线交AD于F.

求证:BE=EF.

2.已知在ΔABC中,∠A的内,外角平分线

分别交ΔABC的外接圆于D,E.

求证:DE垂直平分BC.

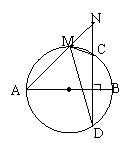
3.AB是⊙O的直径,弦CD⊥AB,M是AC

上一点,延长AM,DC交于N.

求证:∠AMD=∠NMC

(一)填空题

1.圆内的一条弦把圆分成度数之比为1:5的两段弧,则该弦的弦心距与半径之比是______.

2.ΔABC内接于⊙O且BC:AC:AB=3:2:4,则∠A=______度,∠B=______度.

3.　　　　　 ⊙O的一弦AB将⊙O分成1:2的两段弧,则弦AB所对的圆心角是______度,所对的圆周角是______度.

4.　　　　　　 如图:在ΔABC中,∠A=70°,⊙O截

ΔABC的三边,截得的三条弦相等,则

∠BDC=______度.

5.如图:AB是⊙O的直径,半径OC⊥AB,

F是OC中点,弦DE∥AB,且F在DE上,则

∠CBD的度数是______度.

6.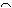已知⊙O中,OA⊥OB,∠A=40°,

则CD的度数是______度.

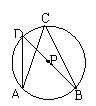
7.如图:∠B=25°,∠APB=80°,

则∠D=______度.

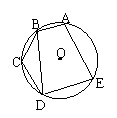
8.如图:已知⊙O的内接五边形ABCDE,

AB=BC=DC,∠BDC=25°,则∠ABD的度数

是______度.

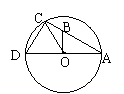
9.如图:AD是直径,B是弦AC上一点,且

OB=5,∠ABC=60°,∠COD=60°,则BC的长

是______.

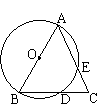
　 10.已知:ΔABC中,AB=AC,以AB为直径

做圆交AC,BC于E,D.∠B=70°,则AE等于

______度,DE等于______度,BD等于______度.

　 11.已知:ΔABC内接于⊙O,⊙O的半径

是6cm,∠B=45°,则AC=______.

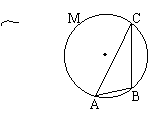
　 12.弦AB等于⊙O的半径,C是AMB

上任一点,则sinC=______.

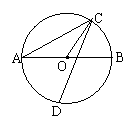
　 13.直径AB和弦CD相交.若AC和BC的度数

比是2:1,D是AB中点,则∠OCD的度数是______度.

1.一条弧上的圆周角等于它所对的圆心角的一半.

推论1:同弧或等弧所对的圆周角相等,在同圆和等圆中,相等的圆周角也相等.此推论是说明在同圆和等圆中,弧等,圆周角等,圆周角相等它们所对的弧相等.在证明中,往往从角找它所对的弧,在从此弧找另一个圆周角,从而证两个圆周角相等.

推论2:直径(半圆)所对的圆周角是直角,90°的圆周角所对的弦是直径.

这个推论一段是若已知是直径,通常做直径上的圆周角,证得是直角.

2.圆周角定理的两个推论很重要.

圆周角定理: